Next Word Suggestion using Graph Neural Network

Language Modeling is a prevalent task in Natural Language Processing. The currently existing most recent and most successful language models often tend to build a massive model with billions of parameters, feed in a tremendous amount of text data, and train with enormous computation resources which require millions of dollars. In this project, we aim to address an important sub-task in language modeling, i.e., context embedding. We propose an approach to exploit the Graph Convolution operation in GNNs to encode the context and use it in coalition with LSTMs to predict the next word given a local context of preceding words. We test this on the custom Wikipedia text corpus using a very limited amount of resources and show that this approach works fairly well to predict the next word.

Verifying Relational Explanations: A Probabilistic Approach

Explanations on relational data are hard to verify since the explanation structures are more complex (e.g. graphs). To verify interpretable explanations (e.g. explanations of predictions made in images, text, etc.), typically human subjects are used since it does not necessarily require a lot of expertise. However, to verify the quality of a relational explanation requires expertise and is hard to scale-up. GNNExplainer is arguably one of the most popular explanation methods for Graph Neural Networks. In this paper, we develop an approach where we assess the uncertainty in explanations generated by GNNExplainer. Specifically, we ask the explainer to generate explanations for several counterfactual examples. We generate these examples as symmetric approximations of the relational structure in the original data. From these explanations, we learn a factor graph model to quantify uncertainty in an explanation. Our results on several datasets show that our approach can help verify explanations from GNNExplainer by reliably estimating the uncertainty of a relation specified in the explanation.

On the verification of Embeddings using Hybrid Markov Logic

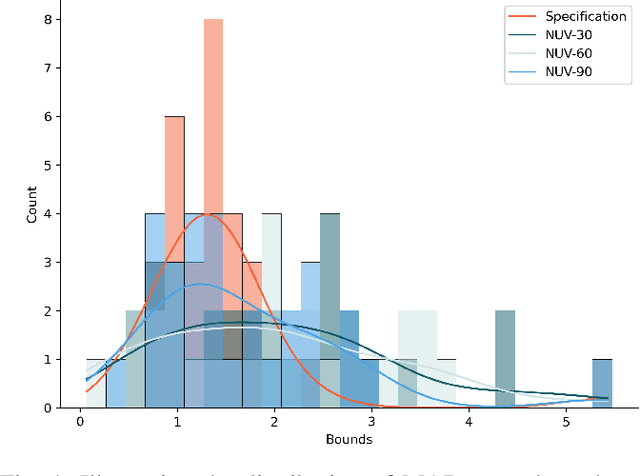
The standard approach to verify representations learned by Deep Neural Networks is to use them in specific tasks such as classification or regression, and measure their performance based on accuracy in such tasks. However, in many cases, we would want to verify more complex properties of a learned representation. To do this, we propose a framework based on a probabilistic first-order language, namely, Hybrid Markov Logic Networks (HMLNs) where we specify properties over embeddings mixed with symbolic domain knowledge. We present an approach to learn parameters for the properties within this framework. Further, we develop a verification method to test embeddings in this framework by encoding this task as a Mixed Integer Linear Program for which we can leverage existing state-of-the-art solvers. We illustrate verification in Graph Neural Networks, Deep Knowledge Tracing and Intelligent Tutoring Systems to demonstrate the generality of our approach.