Correlation Clustering of Organoid Images

In biological and medical research, scientists now routinely acquire microscopy images of hundreds of morphologically heterogeneous organoids and are then faced with the task of finding patterns in the image collection, i.e., subsets of organoids that appear similar and potentially represent the same morphological class. We adopt models and algorithms for correlating organoid images, i.e., for quantifying the similarity in appearance and geometry of the organoids they depict, and for clustering organoid images by consolidating conflicting correlations. For correlating organoid images, we adopt and compare two alternatives, a partial quadratic assignment problem and a twin network. For clustering organoid images, we employ the correlation clustering problem. Empirically, we learn the parameters of these models, infer a clustering of organoid images, and quantify the accuracy of the inferred clusters, with respect to a training set and a test set we contribute of state-of-the-art light microscopy images of organoids clustered manually by biologists.

LiGNN: Graph Neural Networks at LinkedIn

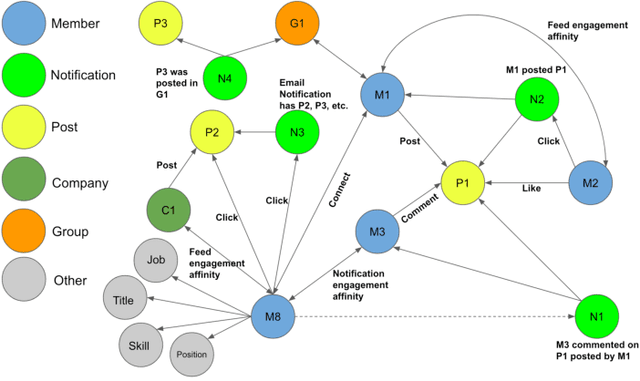
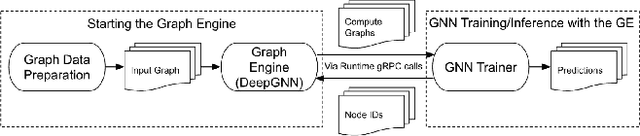
In this paper, we present LiGNN, a deployed large-scale Graph Neural Networks (GNNs) Framework. We share our insight on developing and deployment of GNNs at large scale at LinkedIn. We present a set of algorithmic improvements to the quality of GNN representation learning including temporal graph architectures with long term losses, effective cold start solutions via graph densification, ID embeddings and multi-hop neighbor sampling. We explain how we built and sped up by 7x our large-scale training on LinkedIn graphs with adaptive sampling of neighbors, grouping and slicing of training data batches, specialized shared-memory queue and local gradient optimization. We summarize our deployment lessons and learnings gathered from A/B test experiments. The techniques presented in this work have contributed to an approximate relative improvements of 1% of Job application hearing back rate, 2% Ads CTR lift, 0.5% of Feed engaged daily active users, 0.2% session lift and 0.1% weekly active user lift from people recommendation. We believe that this work can provide practical solutions and insights for engineers who are interested in applying Graph neural networks at large scale.

Correlation Clustering of Bird Sounds

Bird sound classification is the task of relating any sound recording to those species of bird that can be heard in the recording. Here, we study bird sound clustering, the task of deciding for any pair of sound recordings whether the same species of bird can be heard in both. We address this problem by first learning, from a training set, probabilities of pairs of recordings being related in this way, and then inferring a maximally probable partition of a test set by correlation clustering. We address the following questions: How accurate is this clustering, compared to a classification of the test set? How do the clusters thus inferred relate to the clusters obtained by classification? How accurate is this clustering when applied to recordings of bird species not heard during training? How effective is this clustering in separating, from bird sounds, environmental noise not heard during training?

Partial Optimality in Cubic Correlation Clustering

The higher-order correlation clustering problem is an expressive model, and recently, local search heuristics have been proposed for several applications. Certifying optimality, however, is NP-hard and practically hampered already by the complexity of the problem statement. Here, we focus on establishing partial optimality conditions for the special case of complete graphs and cubic objective functions. In addition, we define and implement algorithms for testing these conditions and examine their effect numerically, on two datasets.

Inapproximability of Minimizing a Pair of DNFs or Binary Decision Trees Defining a Partial Boolean Function

The desire to apply machine learning techniques in safety-critical environments has renewed interest in the learning of partial functions for distinguishing between positive, negative and unclear observations. We contribute to the understanding of the hardness of this problem. Specifically, we consider partial Boolean functions defined by a pair of Boolean functions $f, g \colon \{0,1\}^J \to \{0,1\}$ such that $f \cdot g = 0$ and such that $f$ and $g$ are defined by disjunctive normal forms or binary decision trees. We show: Minimizing the sum of the lengths or depths of these forms while separating disjoint sets $A \cup B = S \subseteq \{0,1\}^J$ such that $f(A) = \{1\}$ and $g(B) = \{1\}$ is inapproximable to within $(1 - \epsilon) \ln (|S|-1)$ for any $\epsilon > 0$, unless P=NP.