Least-Squares-Embedded Optimization for Accelerated Convergence of PINNs in Acoustic Wavefield Simulations

Physics-Informed Neural Networks (PINNs) have shown promise in solving partial differential equations (PDEs), including the frequency-domain Helmholtz equation. However, standard training of PINNs using gradient descent (GD) suffers from slow convergence and instability, particularly for high-frequency wavefields. For scattered acoustic wavefield simulation based on Helmholtz equation, we derive a hybrid optimization framework that accelerates training convergence by embedding a least-squares (LS) solver directly into the GD loss function. This formulation enables optimal updates for the linear output layer. Our method is applicable with or without perfectly matched layers (PML), and we provide practical tensor-based implementations for both scenarios. Numerical experiments on benchmark velocity models demonstrate that our approach achieves faster convergence, higher accuracy, and improved stability compared to conventional PINN training. In particular, our results show that the LS-enhanced method converges rapidly even in cases where standard GD-based training fails. The LS solver operates on a small normal matrix, ensuring minimal computational overhead and making the method scalable for large-scale wavefield simulations.

Gabor-Enhanced Physics-Informed Neural Networks for Fast Simulations of Acoustic Wavefields

Physics-Informed Neural Networks (PINNs) have gained increasing attention for solving partial differential equations, including the Helmholtz equation, due to their flexibility and mesh-free formulation. However, their low-frequency bias limits their accuracy and convergence speed for high-frequency wavefield simulations. To alleviate these problems, we propose a simplified PINN framework that incorporates Gabor functions, designed to capture the oscillatory and localized nature of wavefields more effectively. Unlike previous attempts that rely on auxiliary networks to learn Gabor parameters, we redefine the network's task to map input coordinates to a custom Gabor coordinate system, simplifying the training process without increasing the number of trainable parameters compared to a simple PINN. We validate the proposed method across multiple velocity models, including the complex Marmousi and Overthrust models, and demonstrate its superior accuracy, faster convergence, and better robustness features compared to both traditional PINNs and earlier Gabor-based PINNs. Additionally, we propose an efficient integration of a Perfectly Matched Layer (PML) to enhance wavefield behavior near the boundaries. These results suggest that our approach offers an efficient and accurate alternative for scattered wavefield modeling and lays the groundwork for future improvements in PINN-based seismic applications.

Reducing Spatial Discretization Error on Coarse CFD Simulations Using an OpenFOAM-Embedded Deep Learning Framework

We propose a method for reducing the spatial discretization error of coarse computational fluid dynamics (CFD) problems by enhancing the quality of low-resolution simulations using a deep learning model fed with high-quality data. We substitute the default differencing scheme for the convection term by a feed-forward neural network that interpolates velocities from cell centers to face values to produce velocities that approximate the fine-mesh data well. The deep learning framework incorporates the open-source CFD code OpenFOAM, resulting in an end-to-end differentiable model. We automatically differentiate the CFD physics using a discrete adjoint code version. We present a fast communication method between TensorFlow (Python) and OpenFOAM (c++) that accelerates the training process. We applied the model to the flow past a square cylinder problem, reducing the error to about 50% for simulations outside the training distribution compared to the traditional solver in the x- and y-velocity components using an 8x coarser mesh. The training is affordable in terms of time and data samples since the architecture exploits the local features of the physics while generating stable predictions for mid-term simulations.

Residual-based Attention Physics-informed Neural Networks for Efficient Spatio-Temporal Lifetime Assessment of Transformers Operated in Renewable Power Plants

Transformers are vital assets for the reliable and efficient operation of power and energy systems. They support the integration of renewables to the grid through improved grid stability and operation efficiency. Monitoring the health of transformers is essential to ensure grid reliability and efficiency. Thermal insulation ageing is a key transformer failure mode, which is generally tracked by monitoring the hotspot temperature (HST). However, HST measurement is complex and expensive and often estimated from indirect measurements. Existing computationally-efficient HST models focus on space-agnostic thermal models, providing worst-case HST estimates. This article introduces an efficient spatio-temporal model for transformer winding temperature and ageing estimation, which leverages physics-based partial differential equations (PDEs) with data-driven Neural Networks (NN) in a Physics Informed Neural Networks (PINNs) configuration to improve prediction accuracy and acquire spatio-temporal resolution. The computational efficiency of the PINN model is improved through the implementation of the Residual-Based Attention scheme that accelerates the PINN model convergence. PINN based oil temperature predictions are used to estimate spatio-temporal transformer winding temperature values, which are validated through PDE resolution models and fiber optic sensor measurements, respectively. Furthermore, the spatio-temporal transformer ageing model is inferred, aiding transformer health management decision-making and providing insights into localized thermal ageing phenomena in the transformer insulation. Results are validated with a distribution transformer operated on a floating photovoltaic power plant.

Machine Learning Discovery of Optimal Quadrature Rules for Isogeometric Analysis

We propose the use of machine learning techniques to find optimal quadrature rules for the construction of stiffness and mass matrices in isogeometric analysis (IGA). We initially consider 1D spline spaces of arbitrary degree spanned over uniform and non-uniform knot sequences, and then the generated optimal rules are used for integration over higher-dimensional spaces using tensor product sense. The quadrature rule search is posed as an optimization problem and solved by a machine learning strategy based on gradient-descent. However, since the optimization space is highly non-convex, the success of the search strongly depends on the number of quadrature points and the parameter initialization. Thus, we use a dynamic programming strategy that initializes the parameters from the optimal solution over the spline space with a lower number of knots. With this method, we found optimal quadrature rules for spline spaces when using IGA discretizations with up to 50 uniform elements and polynomial degrees up to 8, showing the generality of the approach in this scenario. For non-uniform partitions, the method also finds an optimal rule in a reasonable number of test cases. We also assess the generated optimal rules in two practical case studies, namely, the eigenvalue problem of the Laplace operator and the eigenfrequency analysis of freeform curved beams, where the latter problem shows the applicability of the method to curved geometries. In particular, the proposed method results in savings with respect to traditional Gaussian integration of up to 44% in 1D, 68% in 2D, and 82% in 3D spaces.

A Deep Double Ritz Method for solving Partial Differential Equations using Neural Networks

Residual minimization is a widely used technique for solving Partial Differential Equations in variational form. It minimizes the dual norm of the residual, which naturally yields a saddle-point (min-max) problem over the so-called trial and test spaces. In the context of neural networks, we can address this min-max approach by employing one network to seek the trial minimum, while another network seeks the test maximizers. However, the resulting method is numerically unstable as we approach the trial solution. To overcome this, we reformulate the residual minimization as an equivalent minimization of a Ritz functional fed by optimal test functions computed from another Ritz functional minimization. We call the resulting scheme the Deep Double Ritz Method (D$^2$RM), which combines two neural networks for approximating trial functions and optimal test functions along a nested double Ritz minimization strategy. Numerical results on several 1D diffusion and convection problems support the robustness of our method, up to the approximation properties of the networks and the training capacity of the optimizers.

Deep-Learning Inversion Method for the Interpretation of Noisy Logging-While-Drilling Resistivity Measurements

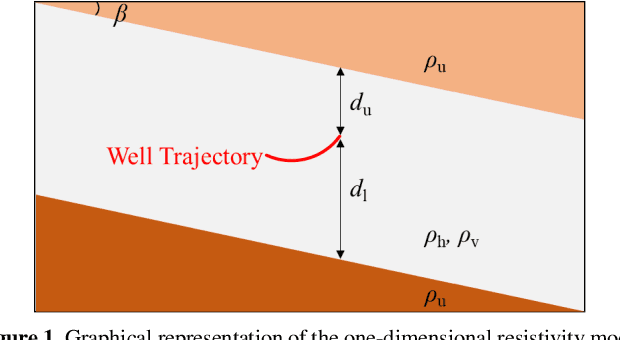
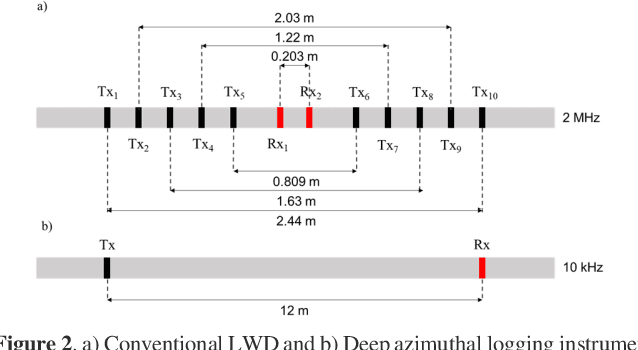
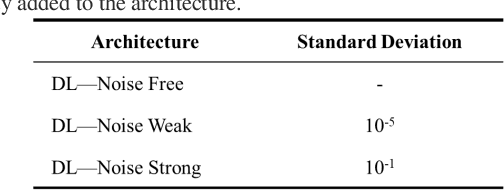
Deep Learning (DL) inversion is a promising method for real time interpretation of logging while drilling (LWD) resistivity measurements for well navigation applications. In this context, measurement noise may significantly affect inversion results. Existing publications examining the effects of measurement noise on DL inversion results are scarce. We develop a method to generate training data sets and construct DL architectures that enhance the robustness of DL inversion methods in the presence of noisy LWD resistivity measurements. We use two synthetic resistivity models to test three approaches that explicitly consider the presence of noise: (1) adding noise to the measurements in the training set, (2) augmenting the training set by replicating it and adding varying noise realizations, and (3) adding a noise layer in the DL architecture. Numerical results confirm that the three approaches produce a denoising effect, yielding better inversion results in both predicted earth model and measurements compared not only to the basic DL inversion but also to traditional gradient based inversion results. A combination of the second and third approaches delivers the best results. The proposed methods can be readily generalized to multi dimensional DL inversion.

Modeling extra-deep EM logs using a deep neural network

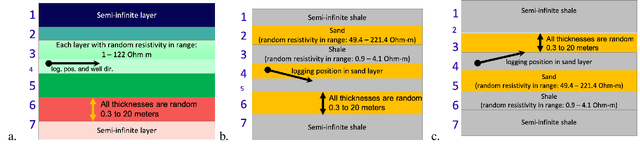
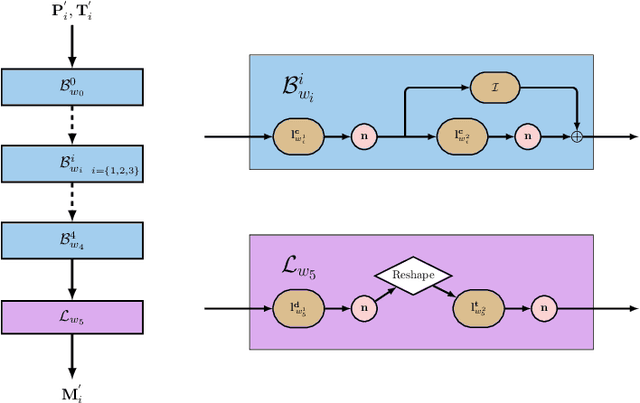
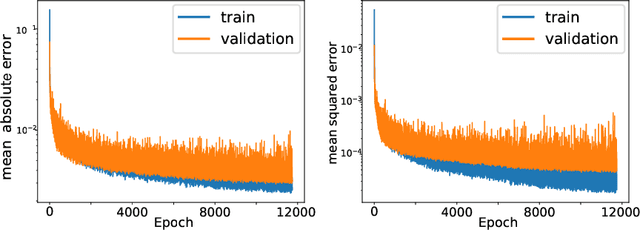
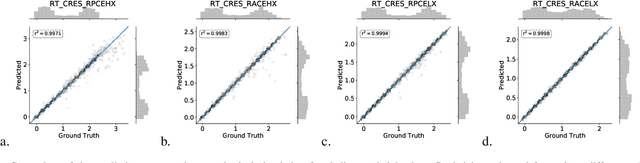
Modern geosteering is heavily dependent on real-time interpretation of deep electromagnetic (EM) measurements. This work presents a deep neural network (DNN) model trained to reproduce the full set of extra-deep real-time EM logs consisting of 22 measurements per logging position. The model is trained in a 1D layered environment and has sensitivity for up to seven layers with different resistivity values. A commercial simulator provided by a tool vendor is utilized to generate a training dataset. The impossibility of parallel execution of the simulator effectively limits the permissible dataset size. Therefore, the geological rules and geosteering specifics supported by the forward model are embraced when designing the dataset. It is then used to produce a fully parallel EM simulator based on a DNN without access to the proprietary information about the EM tool configuration or the original simulator source code. Despite a relatively small training set size, the resulting DNN forward model is quite accurate for synthetic geosteering cases, yet independent of the logging instrument vendor. The observed average evaluation time of 0.15 milliseconds per logging position makes it also suitable for future use as part of evaluation-hungry statistical and/or Monte-Carlo inversion algorithms.