Residual-based Attention Physics-informed Neural Networks for Efficient Spatio-Temporal Lifetime Assessment of Transformers Operated in Renewable Power Plants

Transformers are vital assets for the reliable and efficient operation of power and energy systems. They support the integration of renewables to the grid through improved grid stability and operation efficiency. Monitoring the health of transformers is essential to ensure grid reliability and efficiency. Thermal insulation ageing is a key transformer failure mode, which is generally tracked by monitoring the hotspot temperature (HST). However, HST measurement is complex and expensive and often estimated from indirect measurements. Existing computationally-efficient HST models focus on space-agnostic thermal models, providing worst-case HST estimates. This article introduces an efficient spatio-temporal model for transformer winding temperature and ageing estimation, which leverages physics-based partial differential equations (PDEs) with data-driven Neural Networks (NN) in a Physics Informed Neural Networks (PINNs) configuration to improve prediction accuracy and acquire spatio-temporal resolution. The computational efficiency of the PINN model is improved through the implementation of the Residual-Based Attention scheme that accelerates the PINN model convergence. PINN based oil temperature predictions are used to estimate spatio-temporal transformer winding temperature values, which are validated through PDE resolution models and fiber optic sensor measurements, respectively. Furthermore, the spatio-temporal transformer ageing model is inferred, aiding transformer health management decision-making and providing insights into localized thermal ageing phenomena in the transformer insulation. Results are validated with a distribution transformer operated on a floating photovoltaic power plant.

Quantized Hodgkin-Huxley Model for Quantum Neurons

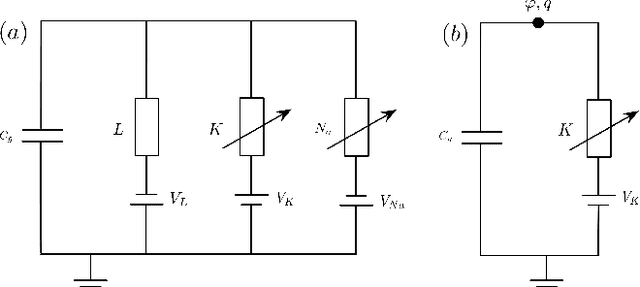
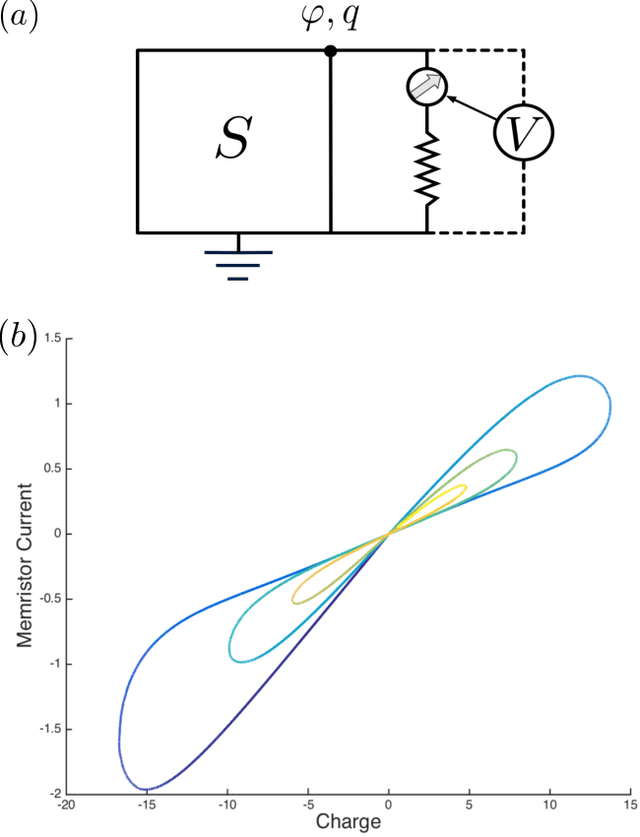
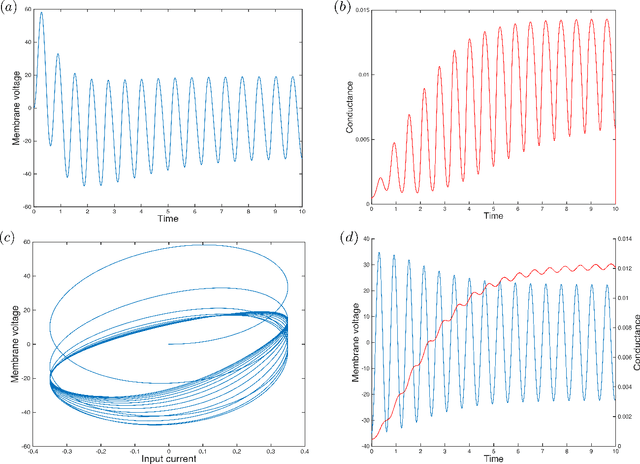
The Hodgkin-Huxley model describes the behavior of the membrane voltage in neurons, treating each element of the cell membrane as an electric circuit element, namely capacitors, memristors and voltage sources. We focus on the activation channel of potassium ions, since it is simpler, while keeping the majority of the features identified with the original Hodgkin-Huxley model. This reduces to a memristor, a resistor whose resistance depends on the history of electric signals that have crossed it, coupled to a voltage source and a capacitor. Here, we take advantage of the recent quantization of the memristor to look into the Hodgkin-Huxley model in the quantum regime. We compare the behavior of the membrane voltage and the potassium channel conductance in both the classical and quantum realms, subjected to AC sources. Numerical simulations show an expected increment and adaptation depending on the history of signals in all regimes. We find that the response of this circuit can be reproduced classically; however, when computing higher moments of the voltage, we encounter purely quantum terms related to the zero-point energy of the circuit. This result paves the way for the construction of quantum neuron networks inspired in the brain function but capable of dealing with quantum information. This could be considered a step forward towards the design of neuromorphic quantum architectures with direct applications in quantum machine learning.

Experimental Implementation of a Quantum Autoencoder via Quantum Adders

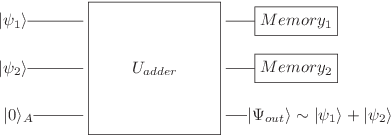
Quantum autoencoders allow for reducing the amount of resources in a quantum computation by mapping the original Hilbert space onto a reduced space with the relevant information. Recently, it was proposed to employ approximate quantum adders to implement quantum autoencoders in quantum technologies. Here, we carry out the experimental implementation of this proposal in the Rigetti cloud quantum computer employing up to three qubits. The experimental fidelities are in good agreement with the theoretical prediction, thus proving the feasibility to realize quantum autoencoders via quantum adders in state-of-the-art superconducting quantum technologies.

Perceptrons from Memristors

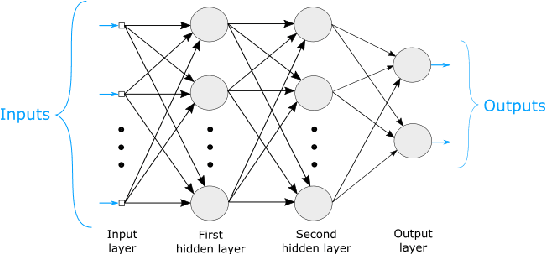
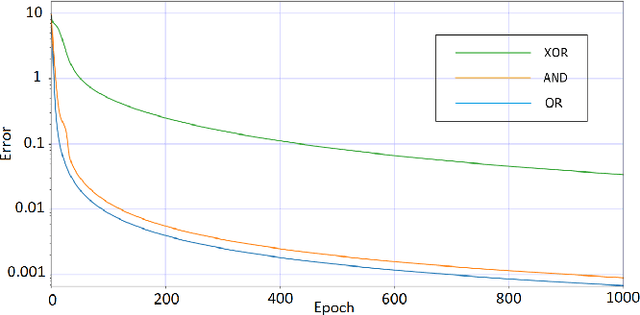
Memristors, resistors with memory whose outputs depend on the history of their inputs, have been used with success in neuromorphic architectures, particularly as synapses or non-volatile memories. A neural network based on memristors could show advantages in terms of energy conservation and open up possibilities for other learning systems to be adapted to a memristor-based paradigm, both in the classical and quantum learning realms. No model for such a network has been proposed so far. Therefore, in order to fill this gap, we introduce models for single and multilayer perceptrons based on memristors. We adapt the delta rule to the memristor-based single-layer perceptron and the backpropagation algorithm to the memristor-based multilayer perceptron. We ran simulations of both the models and the training algorithms. These showed that both of them perform well and in accordance with Minsky-Papert's theorem, which motivates the possibility of building memristor-based hardware for a physical neural network.