Physics-Informed Neural Networks for an optimal counterdiabatic quantum computation

We introduce a novel methodology that leverages the strength of Physics-Informed Neural Networks (PINNs) to address the counterdiabatic (CD) protocol in the optimization of quantum circuits comprised of systems with $N_{Q}$ qubits. The primary objective is to utilize physics-inspired deep learning techniques to accurately solve the time evolution of the different physical observables within the quantum system. To accomplish this objective, we embed the necessary physical information into an underlying neural network to effectively tackle the problem. In particular, we impose the hermiticity condition on all physical observables and make use of the principle of least action, guaranteeing the acquisition of the most appropriate counterdiabatic terms based on the underlying physics. The proposed approach offers a dependable alternative to address the CD driving problem, free from the constraints typically encountered in previous methodologies relying on classical numerical approximations. Our method provides a general framework to obtain optimal results from the physical observables relevant to the problem, including the external parameterization in time known as scheduling function, the gauge potential or operator involving the non-adiabatic terms, as well as the temporal evolution of the energy levels of the system, among others. The main applications of this methodology have been the $\mathrm{H_{2}}$ and $\mathrm{LiH}$ molecules, represented by a 2-qubit and 4-qubit systems employing the STO-3G basis. The presented results demonstrate the successful derivation of a desirable decomposition for the non-adiabatic terms, achieved through a linear combination utilizing Pauli operators. This attribute confers significant advantages to its practical implementation within quantum computing algorithms.

Machine Learning for maximizing the memristivity of single and coupled quantum memristors

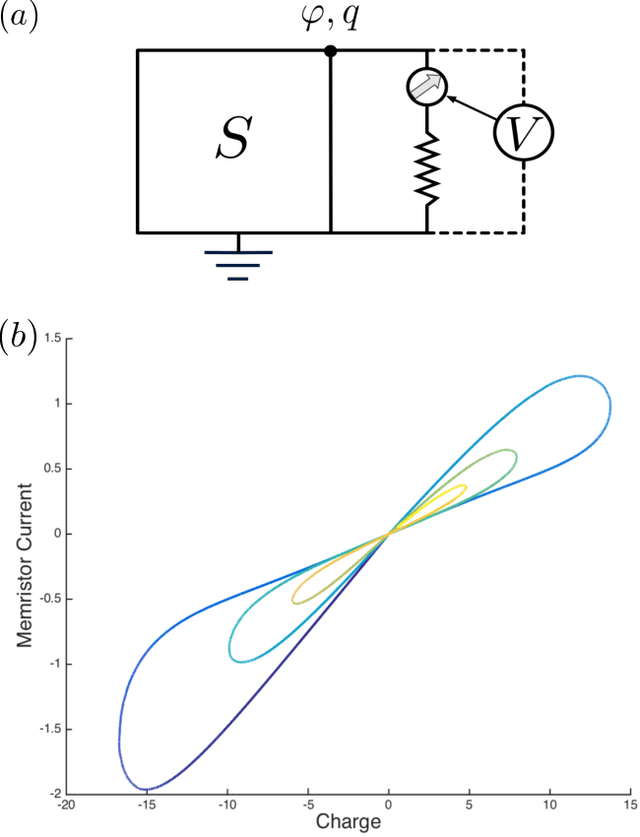
We propose machine learning (ML) methods to characterize the memristive properties of single and coupled quantum memristors. We show that maximizing the memristivity leads to large values in the degree of entanglement of two quantum memristors, unveiling the close relationship between quantum correlations and memory. Our results strengthen the possibility of using quantum memristors as key components of neuromorphic quantum computing.

Quantized Hodgkin-Huxley Model for Quantum Neurons

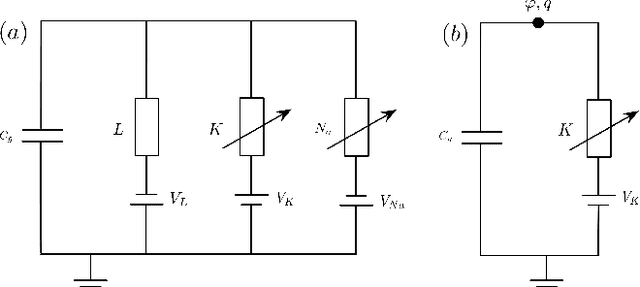
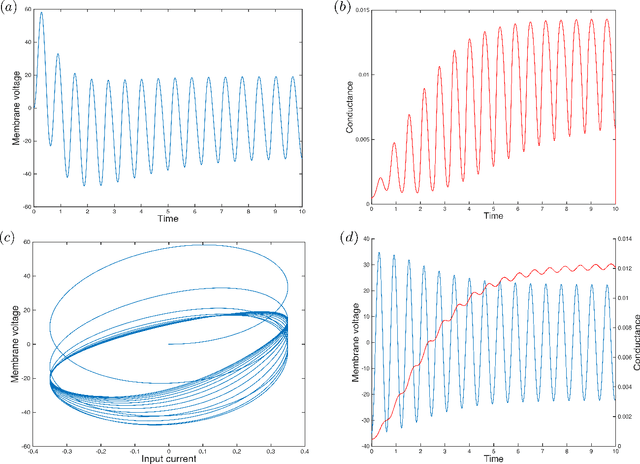
The Hodgkin-Huxley model describes the behavior of the membrane voltage in neurons, treating each element of the cell membrane as an electric circuit element, namely capacitors, memristors and voltage sources. We focus on the activation channel of potassium ions, since it is simpler, while keeping the majority of the features identified with the original Hodgkin-Huxley model. This reduces to a memristor, a resistor whose resistance depends on the history of electric signals that have crossed it, coupled to a voltage source and a capacitor. Here, we take advantage of the recent quantization of the memristor to look into the Hodgkin-Huxley model in the quantum regime. We compare the behavior of the membrane voltage and the potassium channel conductance in both the classical and quantum realms, subjected to AC sources. Numerical simulations show an expected increment and adaptation depending on the history of signals in all regimes. We find that the response of this circuit can be reproduced classically; however, when computing higher moments of the voltage, we encounter purely quantum terms related to the zero-point energy of the circuit. This result paves the way for the construction of quantum neuron networks inspired in the brain function but capable of dealing with quantum information. This could be considered a step forward towards the design of neuromorphic quantum architectures with direct applications in quantum machine learning.

Experimental Implementation of a Quantum Autoencoder via Quantum Adders

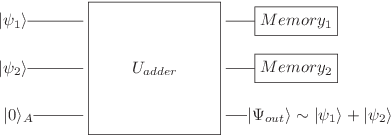
Quantum autoencoders allow for reducing the amount of resources in a quantum computation by mapping the original Hilbert space onto a reduced space with the relevant information. Recently, it was proposed to employ approximate quantum adders to implement quantum autoencoders in quantum technologies. Here, we carry out the experimental implementation of this proposal in the Rigetti cloud quantum computer employing up to three qubits. The experimental fidelities are in good agreement with the theoretical prediction, thus proving the feasibility to realize quantum autoencoders via quantum adders in state-of-the-art superconducting quantum technologies.

Perceptrons from Memristors

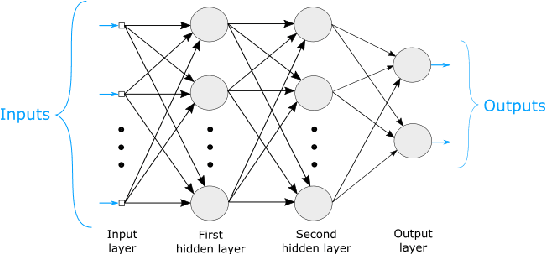
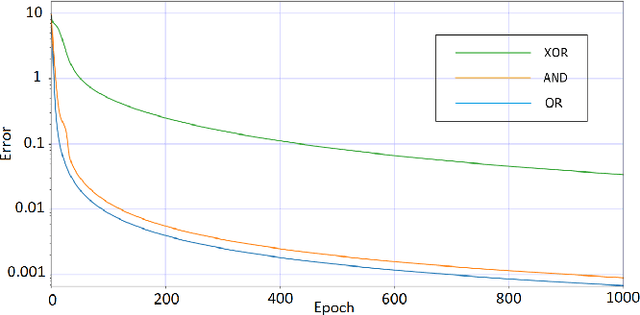
Memristors, resistors with memory whose outputs depend on the history of their inputs, have been used with success in neuromorphic architectures, particularly as synapses or non-volatile memories. A neural network based on memristors could show advantages in terms of energy conservation and open up possibilities for other learning systems to be adapted to a memristor-based paradigm, both in the classical and quantum learning realms. No model for such a network has been proposed so far. Therefore, in order to fill this gap, we introduce models for single and multilayer perceptrons based on memristors. We adapt the delta rule to the memristor-based single-layer perceptron and the backpropagation algorithm to the memristor-based multilayer perceptron. We ran simulations of both the models and the training algorithms. These showed that both of them perform well and in accordance with Minsky-Papert's theorem, which motivates the possibility of building memristor-based hardware for a physical neural network.

Supervised Quantum Learning without Measurements

We propose a quantum machine learning algorithm for efficiently solving a class of problems encoded in quantum controlled unitary operations. The central physical mechanism of the protocol is the iteration of a quantum time-delayed equation that introduces feedback in the dynamics and eliminates the necessity of intermediate measurements. The performance of the quantum algorithm is analyzed by comparing the results obtained in numerical simulations with the outcome of classical machine learning methods for the same problem. The use of time-delayed equations enhances the toolbox of the field of quantum machine learning, which may enable unprecedented applications in quantum technologies.