Quantized Hodgkin-Huxley Model for Quantum Neurons
Paper and Code
Oct 11, 2018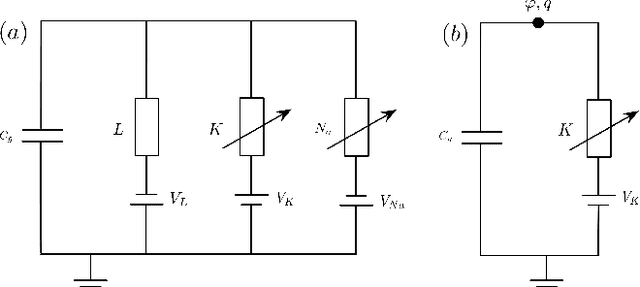
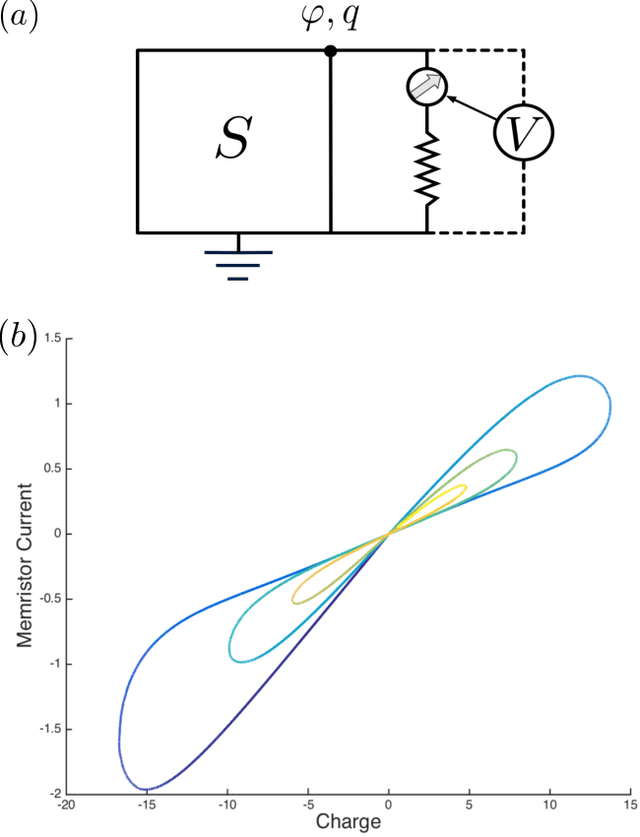
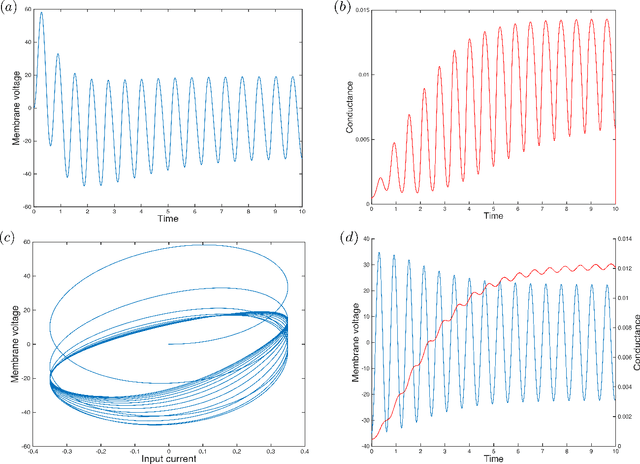
The Hodgkin-Huxley model describes the behavior of the membrane voltage in neurons, treating each element of the cell membrane as an electric circuit element, namely capacitors, memristors and voltage sources. We focus on the activation channel of potassium ions, since it is simpler, while keeping the majority of the features identified with the original Hodgkin-Huxley model. This reduces to a memristor, a resistor whose resistance depends on the history of electric signals that have crossed it, coupled to a voltage source and a capacitor. Here, we take advantage of the recent quantization of the memristor to look into the Hodgkin-Huxley model in the quantum regime. We compare the behavior of the membrane voltage and the potassium channel conductance in both the classical and quantum realms, subjected to AC sources. Numerical simulations show an expected increment and adaptation depending on the history of signals in all regimes. We find that the response of this circuit can be reproduced classically; however, when computing higher moments of the voltage, we encounter purely quantum terms related to the zero-point energy of the circuit. This result paves the way for the construction of quantum neuron networks inspired in the brain function but capable of dealing with quantum information. This could be considered a step forward towards the design of neuromorphic quantum architectures with direct applications in quantum machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge