Quantum Interference for Counting Clusters

Counting the number of clusters, when these clusters overlap significantly is a challenging problem in machine learning. We argue that a purely mathematical quantum theory, formulated using the path integral technique, when applied to non-physics modeling leads to non-physics quantum theories that are statistical in nature. We show that a quantum theory can be a more robust statistical theory to separate data to count overlapping clusters. The theory is also confirmed from data simulations.This works identify how quantum theory can be effective in counting clusters and hope to inspire the field to further apply such techniques.

Fine-Grained Visual Recognition with Batch Confusion Norm

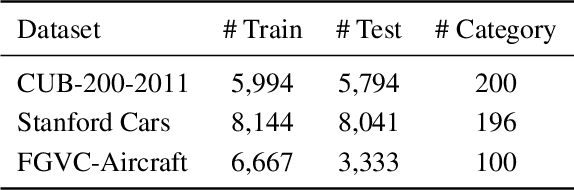
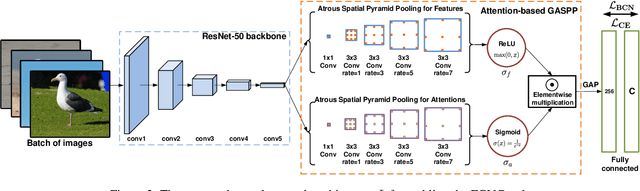
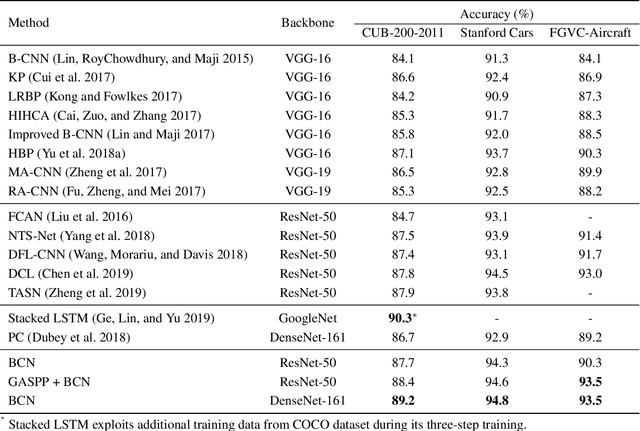
We introduce a regularization concept based on the proposed Batch Confusion Norm (BCN) to address Fine-Grained Visual Classification (FGVC). The FGVC problem is notably characterized by its two intriguing properties, significant inter-class similarity and intra-class variations, which cause learning an effective FGVC classifier a challenging task. Inspired by the use of pairwise confusion energy as a regularization mechanism, we develop the BCN technique to improve the FGVC learning by imposing class prediction confusion on each training batch, and consequently alleviate the possible overfitting due to exploring image feature of fine details. In addition, our method is implemented with an attention gated CNN model, boosted by the incorporation of Atrous Spatial Pyramid Pooling (ASPP) to extract discriminative features and proper attentions. To demonstrate the usefulness of our method, we report state-of-the-art results on several benchmark FGVC datasets, along with comprehensive ablation comparisons.

Quantum Clustering and Gaussian Mixtures

The mixture of Gaussian distributions, a soft version of k-means , is considered a state-of-the-art clustering algorithm. It is widely used in computer vision for selecting classes, e.g., color, texture, and shapes. In this algorithm, each class is described by a Gaussian distribution, defined by its mean and covariance. The data is described by a weighted sum of these Gaussian distributions. We propose a new method, inspired by quantum interference in physics. Instead of modeling each class distribution directly, we model a class wave function such that its magnitude square is the class Gaussian distribution. We then mix the class wave functions to create the mixture wave function. The final mixture distribution is then the magnitude square of the mixture wave function. As a result, we observe the quantum class interference phenomena, not present in the Gaussian mixture model. We show that the quantum method outperforms the Gaussian mixture method in every aspect of the estimations. It provides more accurate estimations of all distribution parameters, with much less fluctuations, and it is also more robust to data deformations from the Gaussian assumptions. We illustrate our method for color segmentation as an example application.

A convolutional approach to reflection symmetry

We present a convolutional approach to reflection symmetry detection in 2D. Our model, built on the products of complex-valued wavelet convolutions, simplifies previous edge-based pairwise methods. Being parameter-centered, as opposed to feature-centered, it has certain computational advantages when the object sizes are known a priori, as demonstrated in an ellipse detection application. The method outperforms the best-performing algorithm on the CVPR 2013 Symmetry Detection Competition Database in the single-symmetry case. Code and a new database for 2D symmetry detection is available.

Complex-Valued Hough Transforms for Circles

This paper advocates the use of complex variables to represent votes in the Hough transform for circle detection. Replacing the positive numbers classically used in the parameter space of the Hough transforms by complex numbers allows cancellation effects when adding up the votes. Cancellation and the computation of shape likelihood via a complex number's magnitude square lead to more robust solutions than the "classic" algorithms, as shown by computational experiments on synthetic and real datasets.

Quantum Pairwise Symmetry: Applications in 2D Shape Analysis

A pair of rooted tangents -- defining a quantum triangle -- with an associated quantum wave of spin 1/2 is proposed as the primitive to represent and compute symmetry. Measures of the spin characterize how "isosceles" or how "degenerate" these triangles are -- which corresponds to their mirror or parallel symmetry. We also introduce a complex-valued kernel to model probability errors in the parameter space, which is more robust to noise and clutter than the classical model.

A Geometric Descriptor for Cell-Division Detection

We describe a method for cell-division detection based on a geometric-driven descriptor that can be represented as a 5-layers processing network, based mainly on wavelet filtering and a test for mirror symmetry between pairs of pixels. After the centroids of the descriptors are computed for a sequence of frames, the two-steps piecewise constant function that best fits the sequence of centroids determines the frame where the division occurs.