Dario Poletti
Tensor-Networks-based Learning of Probabilistic Cellular Automata Dynamics
Apr 17, 2024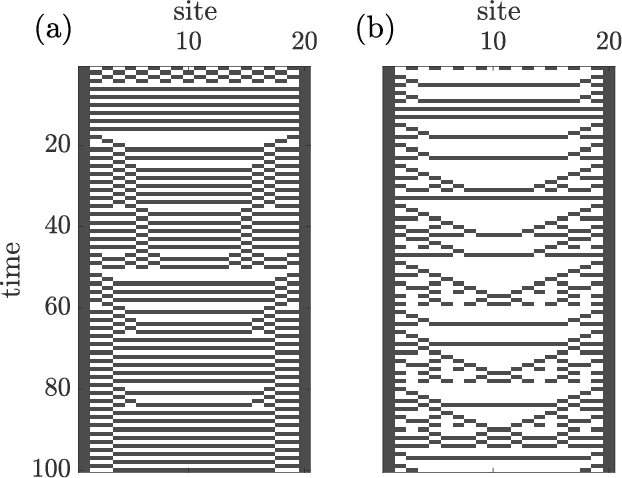
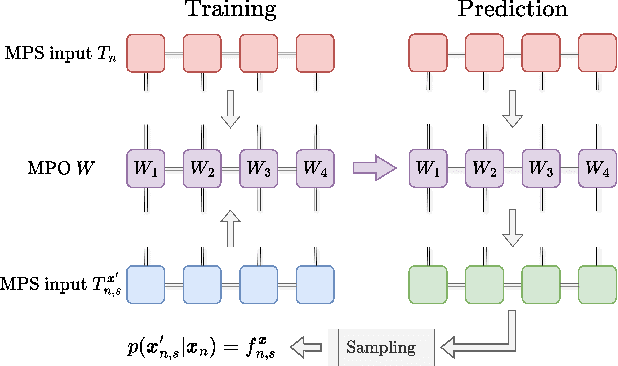
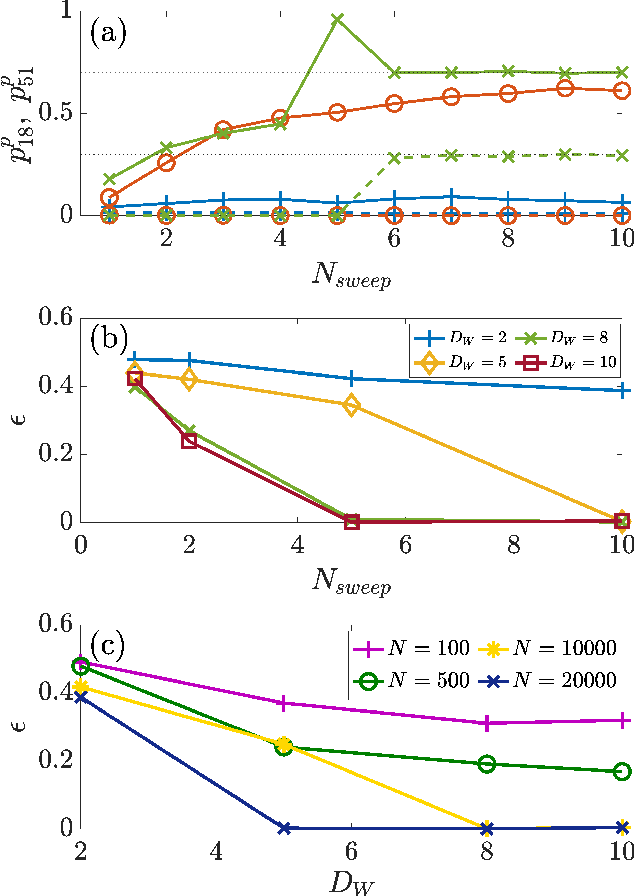
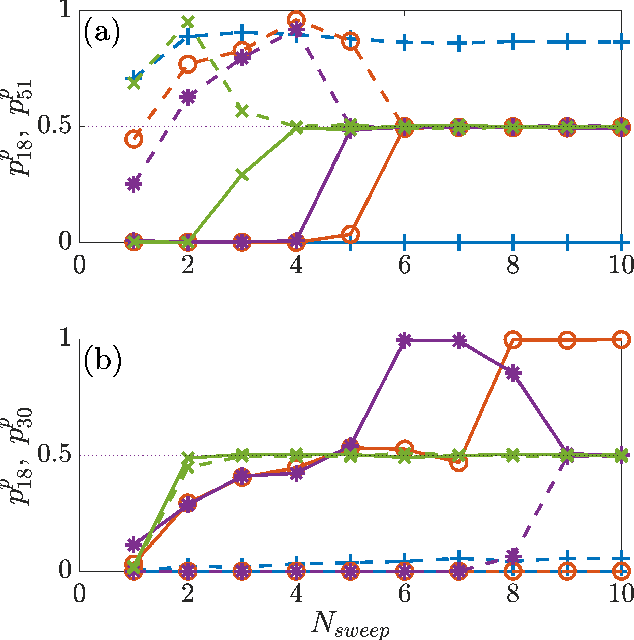
Abstract:Algorithms developed to solve many-body quantum problems, like tensor networks, can turn into powerful quantum-inspired tools to tackle problems in the classical domain. In this work, we focus on matrix product operators, a prominent numerical technique to study many-body quantum systems, especially in one dimension. It has been previously shown that such a tool can be used for classification, learning of deterministic sequence-to-sequence processes and of generic quantum processes. We further develop a matrix product operator algorithm to learn probabilistic sequence-to-sequence processes and apply this algorithm to probabilistic cellular automata. This new approach can accurately learn probabilistic cellular automata processes in different conditions, even when the process is a probabilistic mixture of different chaotic rules. In addition, we find that the ability to learn these dynamics is a function of the bit-wise difference between the rules and whether one is much more likely than the other.
Word2rate: training and evaluating multiple word embeddings as statistical transitions
Apr 16, 2021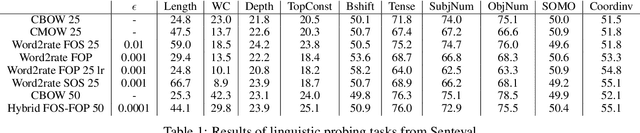
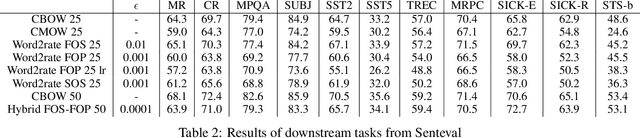
Abstract:Using pretrained word embeddings has been shown to be a very effective way in improving the performance of natural language processing tasks. In fact almost any natural language tasks that can be thought of has been improved by these pretrained embeddings. These tasks range from sentiment analysis, translation, sequence prediction amongst many others. One of the most successful word embeddings is the Word2vec CBOW model proposed by Mikolov trained by the negative sampling technique. Mai et al. modifies this objective to train CMOW embeddings that are sensitive to word order. We used a modified version of the negative sampling objective for our context words, modelling the context embeddings as a Taylor series of rate matrices. We show that different modes of the Taylor series produce different types of embeddings. We compare these embeddings to their similar counterparts like CBOW and CMOW and show that they achieve comparable performance. We also introduce a novel left-right context split objective that improves performance for tasks sensitive to word order. Our Word2rate model is grounded in a statistical foundation using rate matrices while being competitive in variety of language tasks.
A scheme for automatic differentiation of complex loss functions
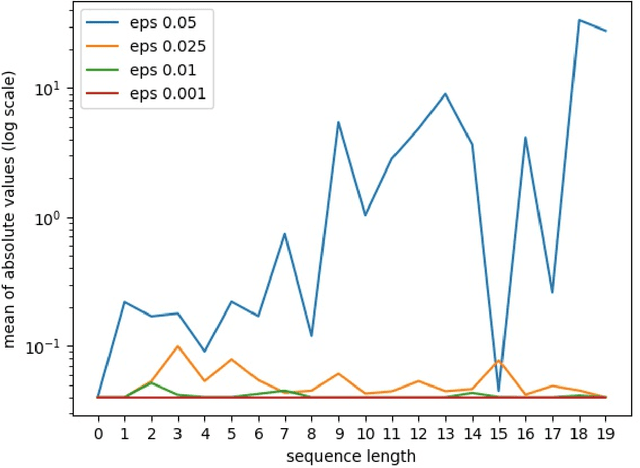
Mar 02, 2020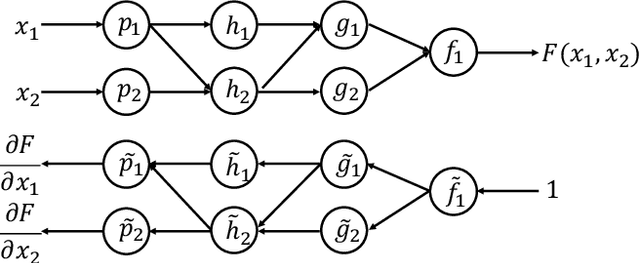

Abstract:For a real function, automatic differentiation is such a standard algorithm used to efficiently compute its gradient, that it is integrated in various neural network frameworks. However, despite the recent advances in using complex functions in machine learning and the well-established usefulness of automatic differentiation, the support of automatic differentiation for complex functions is not as well-established and widespread as for real functions. In this work we propose an efficient and seamless scheme to implement automatic differentiation for complex functions, which is a compatible generalization of the current scheme for real functions. This scheme can significantly simplify the implementation of neural networks which use complex numbers.
Finding Quantum Critical Points with Neural-Network Quantum States
Feb 07, 2020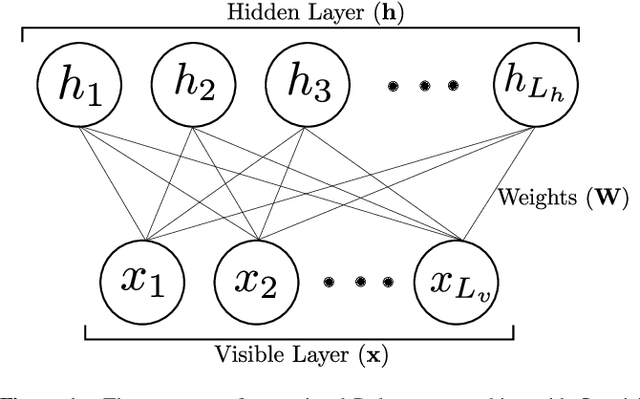
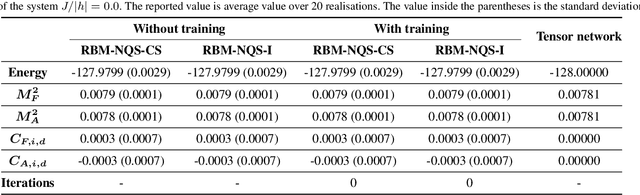
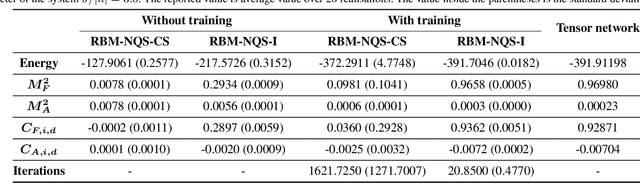
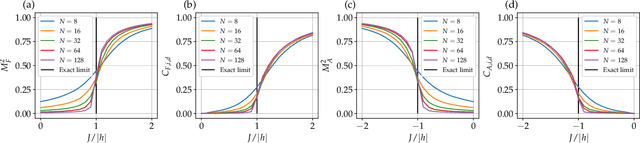
Abstract:Finding the precise location of quantum critical points is of particular importance to characterise quantum many-body systems at zero temperature. However, quantum many-body systems are notoriously hard to study because the dimension of their Hilbert space increases exponentially with their size. Recently, machine learning tools known as neural-network quantum states have been shown to effectively and efficiently simulate quantum many-body systems. We present an approach to finding the quantum critical points of the quantum Ising model using neural-network quantum states, analytically constructed innate restricted Boltzmann machines, transfer learning and unsupervised learning. We validate the approach and evaluate its efficiency and effectiveness in comparison with other traditional approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge