William J. Munro
Tensor-Networks-based Learning of Probabilistic Cellular Automata Dynamics
Apr 17, 2024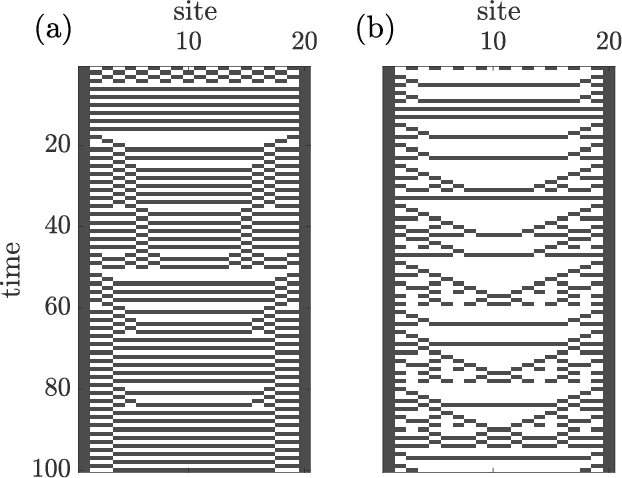
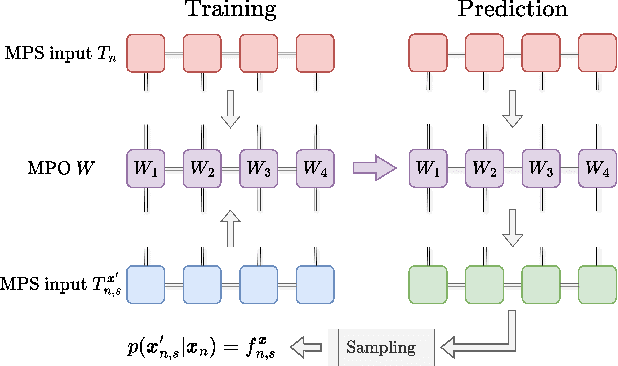
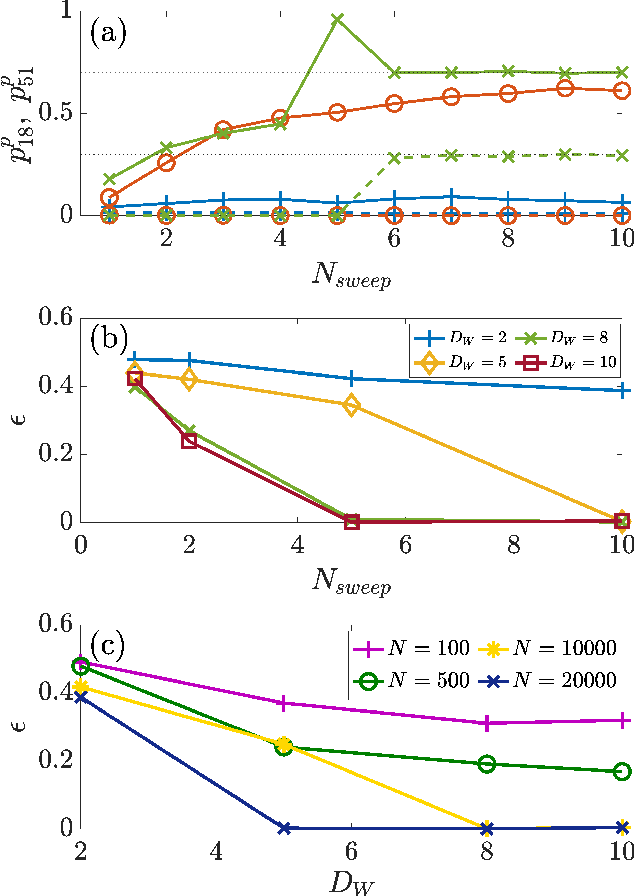
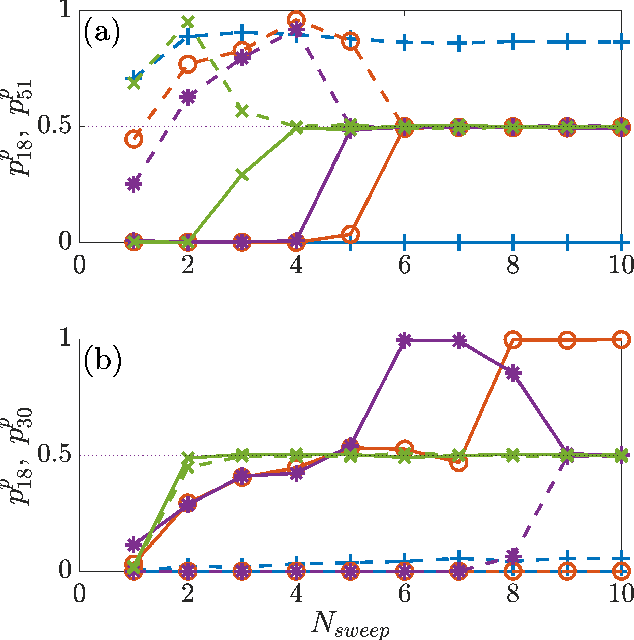
Abstract:Algorithms developed to solve many-body quantum problems, like tensor networks, can turn into powerful quantum-inspired tools to tackle problems in the classical domain. In this work, we focus on matrix product operators, a prominent numerical technique to study many-body quantum systems, especially in one dimension. It has been previously shown that such a tool can be used for classification, learning of deterministic sequence-to-sequence processes and of generic quantum processes. We further develop a matrix product operator algorithm to learn probabilistic sequence-to-sequence processes and apply this algorithm to probabilistic cellular automata. This new approach can accurately learn probabilistic cellular automata processes in different conditions, even when the process is a probabilistic mixture of different chaotic rules. In addition, we find that the ability to learn these dynamics is a function of the bit-wise difference between the rules and whether one is much more likely than the other.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge