A Personalised Learning Tool for Physics Undergraduate Students Built On a Large Language Model for Symbolic Regression

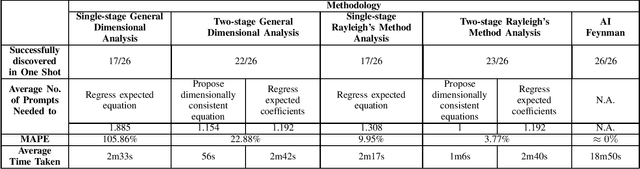
Interleaved practice enhances the memory and problem-solving ability of students in undergraduate courses. We introduce a personalized learning tool built on a Large Language Model (LLM) that can provide immediate and personalized attention to students as they complete homework containing problems interleaved from undergraduate physics courses. Our tool leverages the dimensional analysis method, enhancing students' qualitative thinking and problem-solving skills for complex phenomena. Our approach combines LLMs for symbolic regression with dimensional analysis via prompt engineering and offers students a unique perspective to comprehend relationships between physics variables. This fosters a broader and more versatile understanding of physics and mathematical principles and complements a conventional undergraduate physics education that relies on interpreting and applying established equations within specific contexts. We test our personalized learning tool on the equations from Feynman's lectures on physics. Our tool can correctly identify relationships between physics variables for most equations, underscoring its value as a complementary personalized learning tool for undergraduate physics students.

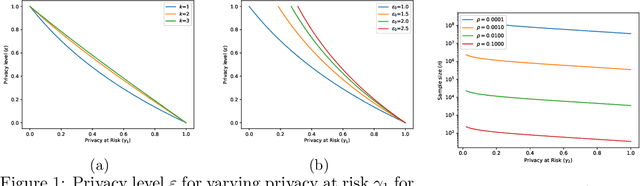
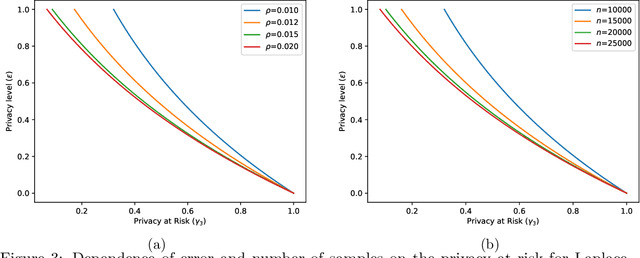
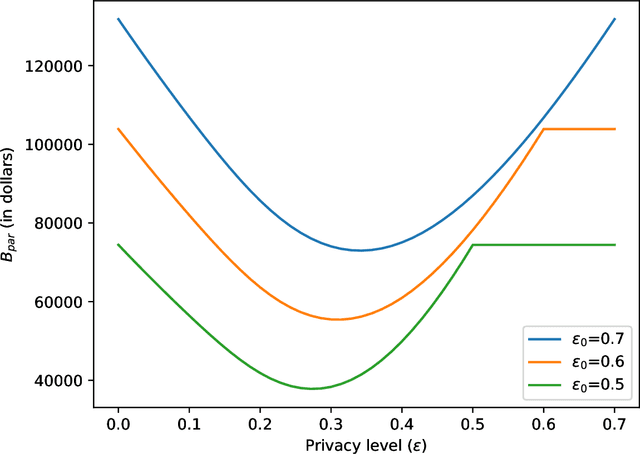
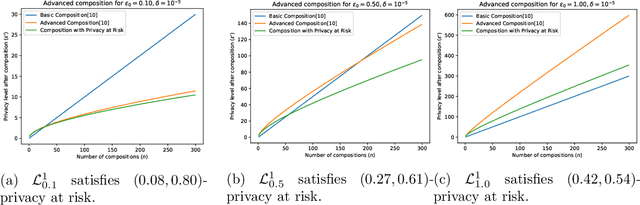
Differential Privacy at Risk: Bridging Randomness and Privacy Budget

The calibration of noise for a privacy-preserving mechanism depends on the sensitivity of the query and the prescribed privacy level. A data steward must make the non-trivial choice of a privacy level that balances the requirements of users and the monetary constraints of the business entity. We analyse roles of the sources of randomness, namely the explicit randomness induced by the noise distribution and the implicit randomness induced by the data-generation distribution, that are involved in the design of a privacy-preserving mechanism. The finer analysis enables us to provide stronger privacy guarantees with quantifiable risks. Thus, we propose privacy at risk that is a probabilistic calibration of privacy-preserving mechanisms. We provide a composition theorem that leverages privacy at risk. We instantiate the probabilistic calibration for the Laplace mechanism by providing analytical results. We also propose a cost model that bridges the gap between the privacy level and the compensation budget estimated by a GDPR compliant business entity. The convexity of the proposed cost model leads to a unique fine-tuning of privacy level that minimises the compensation budget. We show its effectiveness by illustrating a realistic scenario that avoids overestimation of the compensation budget by using privacy at risk for the Laplace mechanism. We quantitatively show that composition using the cost optimal privacy at risk provides stronger privacy guarantee than the classical advanced composition.

Finding Quantum Critical Points with Neural-Network Quantum States

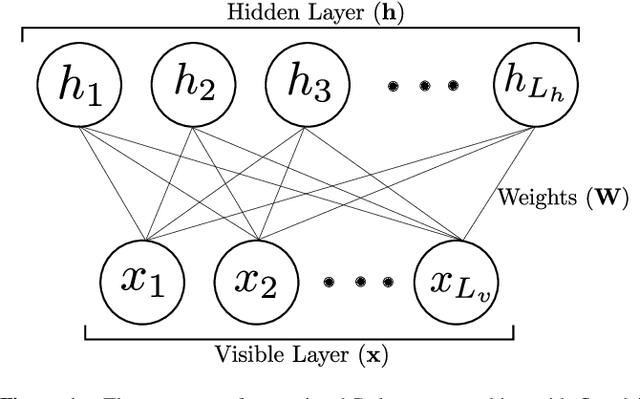
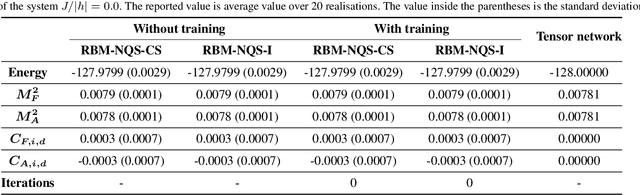
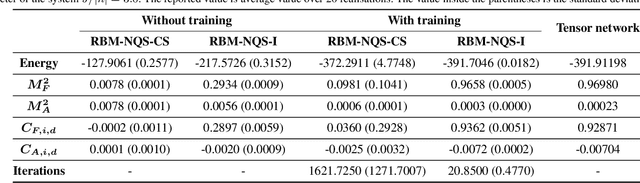
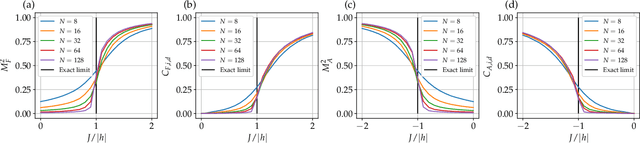
Finding the precise location of quantum critical points is of particular importance to characterise quantum many-body systems at zero temperature. However, quantum many-body systems are notoriously hard to study because the dimension of their Hilbert space increases exponentially with their size. Recently, machine learning tools known as neural-network quantum states have been shown to effectively and efficiently simulate quantum many-body systems. We present an approach to finding the quantum critical points of the quantum Ising model using neural-network quantum states, analytically constructed innate restricted Boltzmann machines, transfer learning and unsupervised learning. We validate the approach and evaluate its efficiency and effectiveness in comparison with other traditional approaches.