Rediscovering the Lunar Equation of the Centre with AI Feynman via Embedded Physical Biases

This work explores using the physics-inspired AI Feynman symbolic regression algorithm to automatically rediscover a fundamental equation in astronomy -- the Equation of the Centre. Through the introduction of observational and inductive biases corresponding to the physical nature of the system through data preprocessing and search space restriction, AI Feynman was successful in recovering the first-order analytical form of this equation from lunar ephemerides data. However, this manual approach highlights a key limitation in its reliance on expert-driven coordinate system selection. We therefore propose an automated preprocessing extension to find the canonical coordinate system. Results demonstrate that targeted domain knowledge embedding enables symbolic regression to rediscover physical laws, but also highlight further challenges in constraining symbolic regression to derive physics equations when leveraging domain knowledge through tailored biases.

Uncovering Scaling Laws for Large Language Models via Inverse Problems

Large Language Models (LLMs) are large-scale pretrained models that have achieved remarkable success across diverse domains. These successes have been driven by unprecedented complexity and scale in both data and computations. However, due to the high costs of training such models, brute-force trial-and-error approaches to improve LLMs are not feasible. Inspired by the success of inverse problems in uncovering fundamental scientific laws, this position paper advocates that inverse problems can also efficiently uncover scaling laws that guide the building of LLMs to achieve the desirable performance with significantly better cost-effectiveness.

Physics-informed Discovery of State Variables in Second-Order and Hamiltonian Systems

The modeling of dynamical systems is a pervasive concern for not only describing but also predicting and controlling natural phenomena and engineered systems. Current data-driven approaches often assume prior knowledge of the relevant state variables or result in overparameterized state spaces. Boyuan Chen and his co-authors proposed a neural network model that estimates the degrees of freedom and attempts to discover the state variables of a dynamical system. Despite its innovative approach, this baseline model lacks a connection to the physical principles governing the systems it analyzes, leading to unreliable state variables. This research proposes a method that leverages the physical characteristics of second-order Hamiltonian systems to constrain the baseline model. The proposed model outperforms the baseline model in identifying a minimal set of non-redundant and interpretable state variables.

A Personalised Learning Tool for Physics Undergraduate Students Built On a Large Language Model for Symbolic Regression

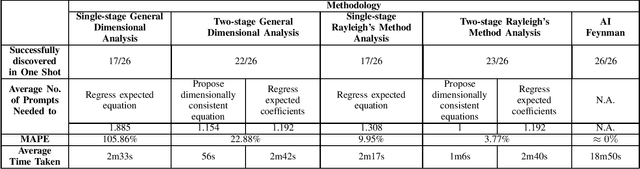
Interleaved practice enhances the memory and problem-solving ability of students in undergraduate courses. We introduce a personalized learning tool built on a Large Language Model (LLM) that can provide immediate and personalized attention to students as they complete homework containing problems interleaved from undergraduate physics courses. Our tool leverages the dimensional analysis method, enhancing students' qualitative thinking and problem-solving skills for complex phenomena. Our approach combines LLMs for symbolic regression with dimensional analysis via prompt engineering and offers students a unique perspective to comprehend relationships between physics variables. This fosters a broader and more versatile understanding of physics and mathematical principles and complements a conventional undergraduate physics education that relies on interpreting and applying established equations within specific contexts. We test our personalized learning tool on the equations from Feynman's lectures on physics. Our tool can correctly identify relationships between physics variables for most equations, underscoring its value as a complementary personalized learning tool for undergraduate physics students.

Celestial Machine Learning: Discovering the Planarity, Heliocentricity, and Orbital Equation of Mars with AI Feynman

Can a machine or algorithm discover or learn the elliptical orbit of Mars from astronomical sightings alone? Johannes Kepler required two paradigm shifts to discover his First Law regarding the elliptical orbit of Mars. Firstly, a shift from the geocentric to the heliocentric frame of reference. Secondly, the reduction of the orbit of Mars from a three- to a two-dimensional space. We extend AI Feynman, a physics-inspired tool for symbolic regression, to discover the heliocentricity and planarity of Mars' orbit and emulate his discovery of Kepler's first law.

A Comparative Evaluation of Additive Separability Tests for Physics-Informed Machine Learning

Many functions characterising physical systems are additively separable. This is the case, for instance, of mechanical Hamiltonian functions in physics, population growth equations in biology, and consumer preference and utility functions in economics. We consider the scenario in which a surrogate of a function is to be tested for additive separability. The detection that the surrogate is additively separable can be leveraged to improve further learning. Hence, it is beneficial to have the ability to test for such separability in surrogates. The mathematical approach is to test if the mixed partial derivative of the surrogate is zero; or empirically, lower than a threshold. We present and comparatively and empirically evaluate the eight methods to compute the mixed partial derivative of a surrogate function.

What's Next? Predicting Hamiltonian Dynamics from Discrete Observations of a Vector Field

We present several methods for predicting the dynamics of Hamiltonian systems from discrete observations of their vector field. Each method is either informed or uninformed of the Hamiltonian property. We empirically and comparatively evaluate the methods and observe that information that the system is Hamiltonian can be effectively informed, and that different methods strike different trade-offs between efficiency and effectiveness for different dynamical systems.

Celestial Machine Learning: From Data to Mars and Beyond with AI Feynman

Can a machine or algorithm discover or learn Kepler's first law from astronomical sightings alone? We emulate Johannes Kepler's discovery of the equation of the orbit of Mars with the Rudolphine tables using AI Feynman, a physics-inspired tool for symbolic regression.

Separable Hamiltonian Neural Networks

The modelling of dynamical systems from discrete observations is a challenge faced by modern scientific and engineering data systems. Hamiltonian systems are one such fundamental and ubiquitous class of dynamical systems. Hamiltonian neural networks are state-of-the-art models that unsupervised-ly regress the Hamiltonian of a dynamical system from discrete observations of its vector field under the learning bias of Hamilton's equations. Yet Hamiltonian dynamics are often complicated, especially in higher dimensions where the state space of the Hamiltonian system is large relative to the number of samples. A recently discovered remedy to alleviate the complexity between state variables in the state space is to leverage the additive separability of the Hamiltonian system and embed that additive separability into the Hamiltonian neural network. Following the nomenclature of physics-informed machine learning, we propose three separable Hamiltonian neural networks. These models embed additive separability within Hamiltonian neural networks. The first model uses additive separability to quadratically scale the amount of data for training Hamiltonian neural networks. The second model embeds additive separability within the loss function of the Hamiltonian neural network. The third model embeds additive separability through the architecture of the Hamiltonian neural network using conjoined multilayer perceptions. We empirically compare the three models against state-of-the-art Hamiltonian neural networks, and demonstrate that the separable Hamiltonian neural networks, which alleviate complexity between the state variables, are more effective at regressing the Hamiltonian and its vector field.