Physics-informed Discovery of State Variables in Second-Order and Hamiltonian Systems

The modeling of dynamical systems is a pervasive concern for not only describing but also predicting and controlling natural phenomena and engineered systems. Current data-driven approaches often assume prior knowledge of the relevant state variables or result in overparameterized state spaces. Boyuan Chen and his co-authors proposed a neural network model that estimates the degrees of freedom and attempts to discover the state variables of a dynamical system. Despite its innovative approach, this baseline model lacks a connection to the physical principles governing the systems it analyzes, leading to unreliable state variables. This research proposes a method that leverages the physical characteristics of second-order Hamiltonian systems to constrain the baseline model. The proposed model outperforms the baseline model in identifying a minimal set of non-redundant and interpretable state variables.

Optimization-Informed Neural Networks

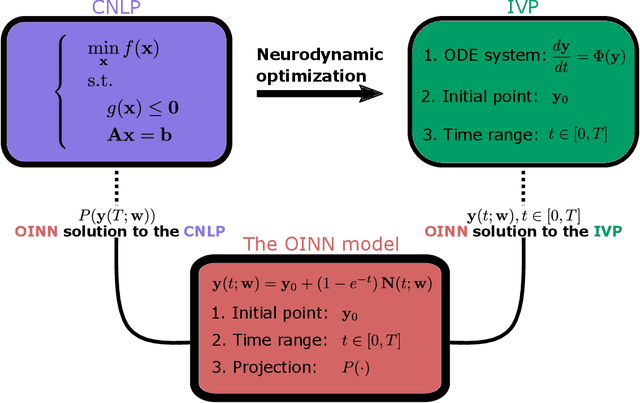
Solving constrained nonlinear optimization problems (CNLPs) is a longstanding problem that arises in various fields, e.g., economics, computer science, and engineering. We propose optimization-informed neural networks (OINN), a deep learning approach to solve CNLPs. By neurodynamic optimization methods, a CNLP is first reformulated as an initial value problem (IVP) involving an ordinary differential equation (ODE) system. A neural network model is then used as an approximate solution for this IVP, with the endpoint being the prediction to the CNLP. We propose a novel training algorithm that directs the model to hold the best prediction during training. In a nutshell, OINN transforms a CNLP into a neural network training problem. By doing so, we can solve CNLPs based on deep learning infrastructure only, without using standard optimization solvers or numerical integration solvers. The effectiveness of the proposed approach is demonstrated through a collection of classical problems, e.g., variational inequalities, nonlinear complementary problems, and standard CNLPs.