Sampling and resolution in sparse view photoacoustic tomography

We investigate resolution in photoacoustic tomography (PAT). Using Shannon theory, we investigate the theoretical resolution limit of sparse view PAT theoretically, and empirically demonstrate that all reconstruction methods used exceed this limit.

Error correcting 2D-3D cascaded network for myocardial infarct scar segmentation on late gadolinium enhancement cardiac magnetic resonance images

Late gadolinium enhancement (LGE) cardiac magnetic resonance (CMR) imaging is considered the in vivo reference standard for assessing infarct size (IS) and microvascular obstruction (MVO) in ST-elevation myocardial infarction (STEMI) patients. However, the exact quantification of those markers of myocardial infarct severity remains challenging and very time-consuming. As LGE distribution patterns can be quite complex and hard to delineate from the blood pool or epicardial fat, automatic segmentation of LGE CMR images is challenging. In this work, we propose a cascaded framework of two-dimensional and three-dimensional convolutional neural networks (CNNs) which enables to calculate the extent of myocardial infarction in a fully automated way. By artificially generating segmentation errors which are characteristic for 2D CNNs during training of the cascaded framework we are enforcing the detection and correction of 2D segmentation errors and hence improve the segmentation accuracy of the entire method. The proposed method was trained and evaluated in a five-fold cross validation using the training dataset from the EMIDEC challenge. We perform comparative experiments where our framework outperforms state-of-the-art methods of the EMIDEC challenge, as well as 2D and 3D nnU-Net. Furthermore, in extensive ablation studies we show the advantages that come with the proposed error correcting cascaded method.

Convergence analysis of equilibrium methods for inverse problems

Recently, the use of deep equilibrium methods has emerged as a new approach for solving imaging and other ill-posed inverse problems. While learned components may be a key factor in the good performance of these methods in practice, a theoretical justification from a regularization point of view is still lacking. In this paper, we address this issue by providing stability and convergence results for the class of equilibrium methods. In addition, we derive convergence rates and stability estimates in the symmetric Bregman distance. We strengthen our results for regularization operators with contractive residuals. Furthermore, we use the presented analysis to gain insight into the practical behavior of these methods, including a lower bound on the performance of the regularized solutions. In addition, we show that the convergence analysis leads to the design of a new type of loss function which has several advantages over previous ones. Numerical simulations are used to support our findings.

Sparse aNETT for Solving Inverse Problems with Deep Learning

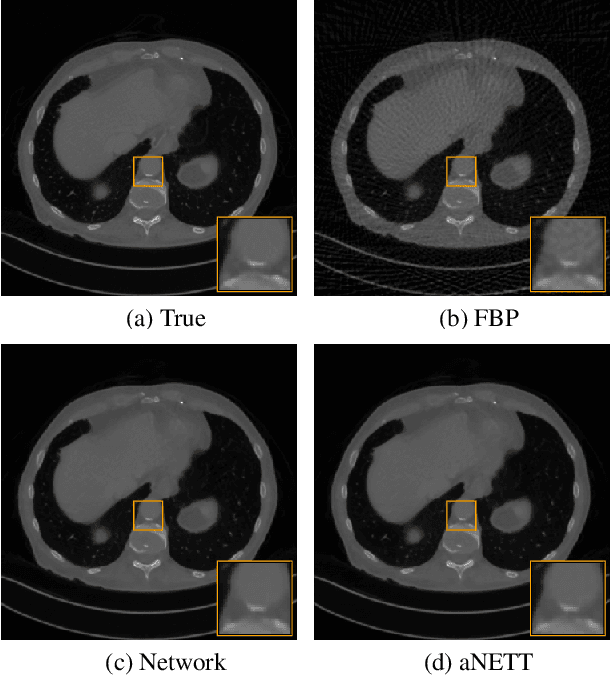
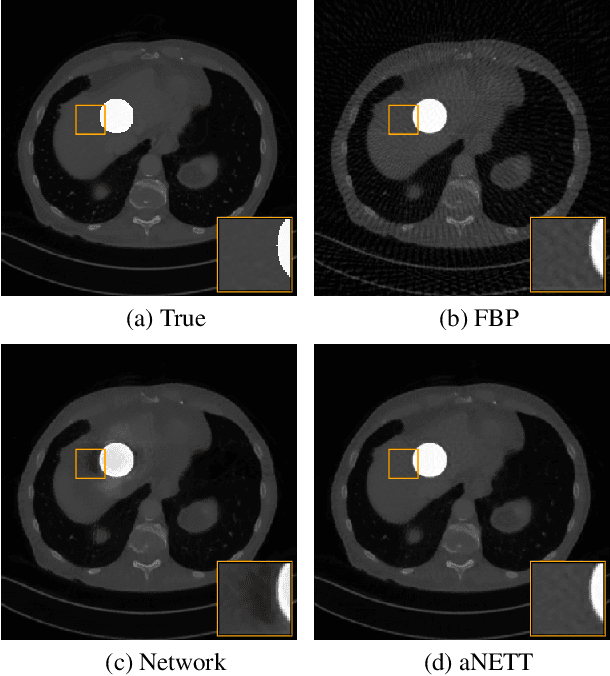
We propose a sparse reconstruction framework (aNETT) for solving inverse problems. Opposed to existing sparse reconstruction techniques that are based on linear sparsifying transforms, we train an autoencoder network $D \circ E$ with $E$ acting as a nonlinear sparsifying transform and minimize a Tikhonov functional with learned regularizer formed by the $\ell^q$-norm of the encoder coefficients and a penalty for the distance to the data manifold. We propose a strategy for training an autoencoder based on a sample set of the underlying image class such that the autoencoder is independent of the forward operator and is subsequently adapted to the specific forward model. Numerical results are presented for sparse view CT, which clearly demonstrate the feasibility, robustness and the improved generalization capability and stability of aNETT over post-processing networks.

Deep synthesis regularization of inverse problems

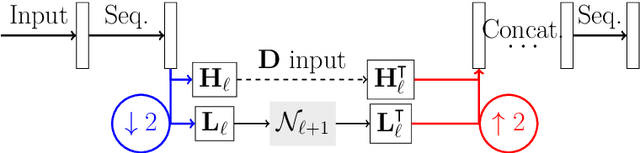
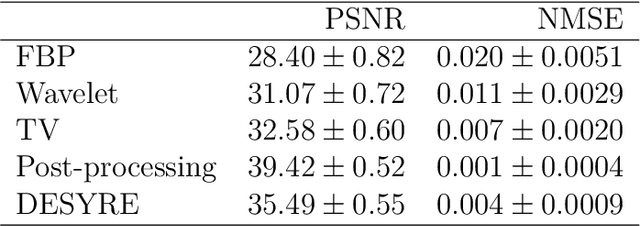
Recently, a large number of efficient deep learning methods for solving inverse problems have been developed and show outstanding numerical performance. For these deep learning methods, however, a solid theoretical foundation in the form of reconstruction guarantees is missing. In contrast, for classical reconstruction methods, such as convex variational and frame-based regularization, theoretical convergence and convergence rate results are well established. In this paper, we introduce deep synthesis regularization (DESYRE) using neural networks as nonlinear synthesis operator bridging the gap between these two worlds. The proposed method allows to exploit the deep learning benefits of being well adjustable to available training data and on the other hand comes with a solid mathematical foundation. We present a complete convergence analysis with convergence rates for the proposed deep synthesis regularization. We present a strategy for constructing a synthesis network as part of an analysis-synthesis sequence together with an appropriate training strategy. Numerical results show the plausibility of our approach.

Sparse $\ell^q$-regularization of inverse problems with deep learning

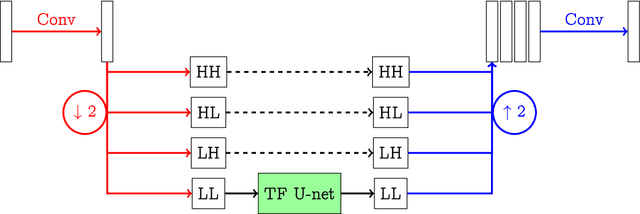
We propose a sparse reconstruction framework for solving inverse problems. Opposed to existing sparse reconstruction techniques that are based on linear sparsifying transforms, we train an encoder-decoder network $D \circ E$ with $E$ acting as a nonlinear sparsifying transform. We minimize a Tikhonov functional which used a learned regularization term formed by the $\ell^q$-norm of the encoder coefficients and a penalty for the distance to the data manifold. For this augmented sparse $\ell^q$-approach, we present a full convergence analysis, derive convergence rates and describe a training strategy. As a main ingredient for the analysis we establish the coercivity of the augmented regularization term.