Sparse $\ell^q$-regularization of inverse problems with deep learning
Paper and Code
Aug 08, 2019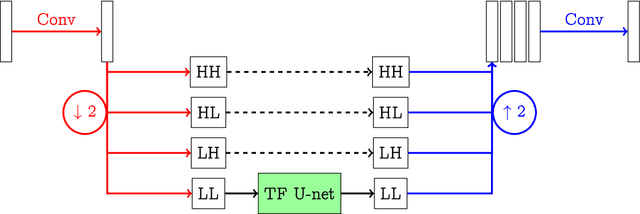
We propose a sparse reconstruction framework for solving inverse problems. Opposed to existing sparse reconstruction techniques that are based on linear sparsifying transforms, we train an encoder-decoder network $D \circ E$ with $E$ acting as a nonlinear sparsifying transform. We minimize a Tikhonov functional which used a learned regularization term formed by the $\ell^q$-norm of the encoder coefficients and a penalty for the distance to the data manifold. For this augmented sparse $\ell^q$-approach, we present a full convergence analysis, derive convergence rates and describe a training strategy. As a main ingredient for the analysis we establish the coercivity of the augmented regularization term.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge