Deep synthesis regularization of inverse problems
Paper and Code
Feb 01, 2020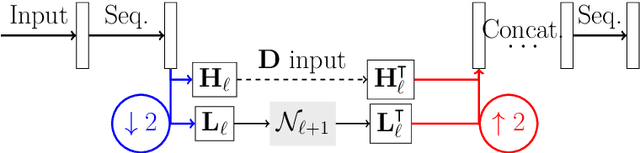


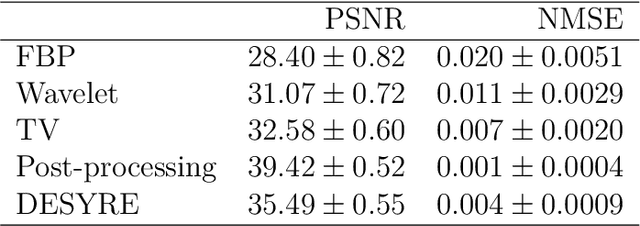
Recently, a large number of efficient deep learning methods for solving inverse problems have been developed and show outstanding numerical performance. For these deep learning methods, however, a solid theoretical foundation in the form of reconstruction guarantees is missing. In contrast, for classical reconstruction methods, such as convex variational and frame-based regularization, theoretical convergence and convergence rate results are well established. In this paper, we introduce deep synthesis regularization (DESYRE) using neural networks as nonlinear synthesis operator bridging the gap between these two worlds. The proposed method allows to exploit the deep learning benefits of being well adjustable to available training data and on the other hand comes with a solid mathematical foundation. We present a complete convergence analysis with convergence rates for the proposed deep synthesis regularization. We present a strategy for constructing a synthesis network as part of an analysis-synthesis sequence together with an appropriate training strategy. Numerical results show the plausibility of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge