Sparse aNETT for Solving Inverse Problems with Deep Learning
Paper and Code
Apr 20, 2020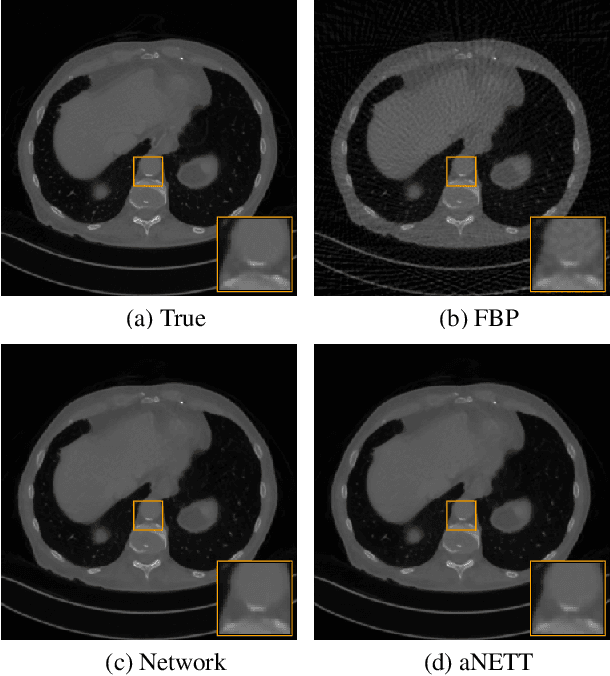


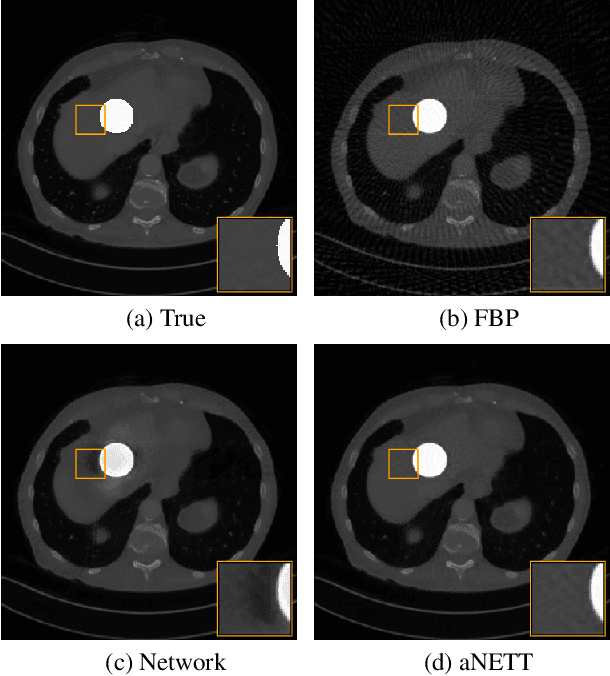
We propose a sparse reconstruction framework (aNETT) for solving inverse problems. Opposed to existing sparse reconstruction techniques that are based on linear sparsifying transforms, we train an autoencoder network $D \circ E$ with $E$ acting as a nonlinear sparsifying transform and minimize a Tikhonov functional with learned regularizer formed by the $\ell^q$-norm of the encoder coefficients and a penalty for the distance to the data manifold. We propose a strategy for training an autoencoder based on a sample set of the underlying image class such that the autoencoder is independent of the forward operator and is subsequently adapted to the specific forward model. Numerical results are presented for sparse view CT, which clearly demonstrate the feasibility, robustness and the improved generalization capability and stability of aNETT over post-processing networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge