Daniel Neill
Lass-0: sparse non-convex regression by local search
Feb 17, 2016

Abstract:We compute approximate solutions to L0 regularized linear regression using L1 regularization, also known as the Lasso, as an initialization step. Our algorithm, the Lass-0 ("Lass-zero"), uses a computationally efficient stepwise search to determine a locally optimal L0 solution given any L1 regularization solution. We present theoretical results of consistency under orthogonality and appropriate handling of redundant features. Empirically, we use synthetic data to demonstrate that Lass-0 solutions are closer to the true sparse support than L1 regularization models. Additionally, in real-world data Lass-0 finds more parsimonious solutions than L1 regularization while maintaining similar predictive accuracy.
Scalable Gaussian Processes for Characterizing Multidimensional Change Surfaces
Nov 13, 2015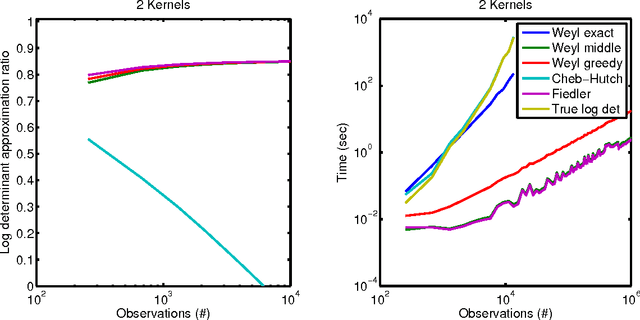
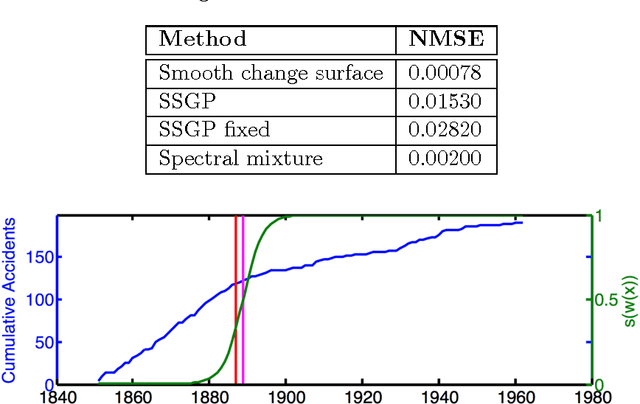
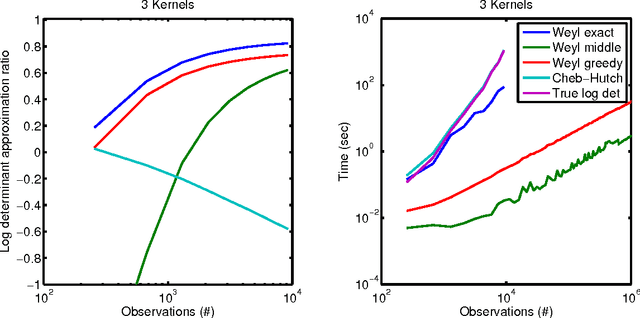
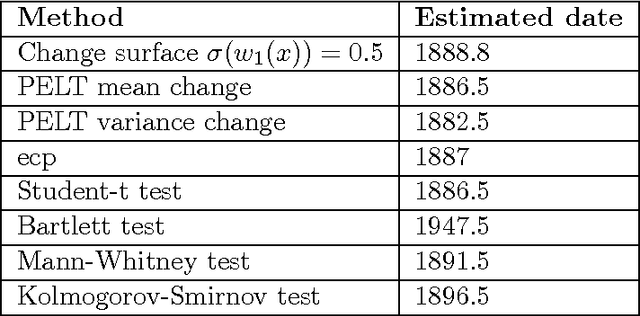
Abstract:We present a scalable Gaussian process model for identifying and characterizing smooth multidimensional changepoints, and automatically learning changes in expressive covariance structure. We use Random Kitchen Sink features to flexibly define a change surface in combination with expressive spectral mixture kernels to capture the complex statistical structure. Finally, through the use of novel methods for additive non-separable kernels, we can scale the model to large datasets. We demonstrate the model on numerical and real world data, including a large spatio-temporal disease dataset where we identify previously unknown heterogeneous changes in space and time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge