Lifted Coefficient of Determination: Fast model-free prediction intervals and likelihood-free model comparison

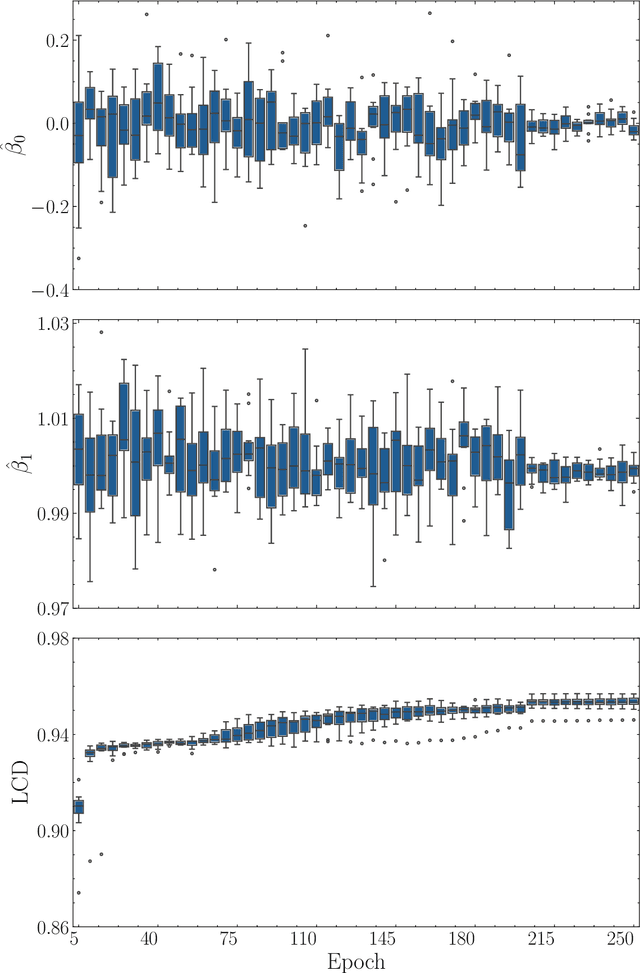
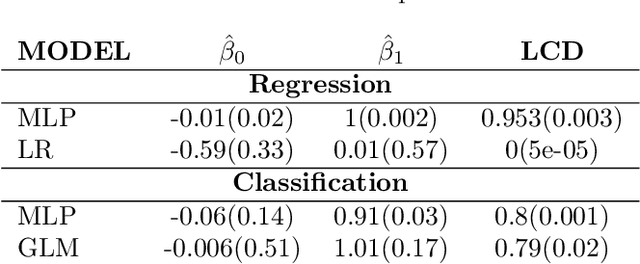
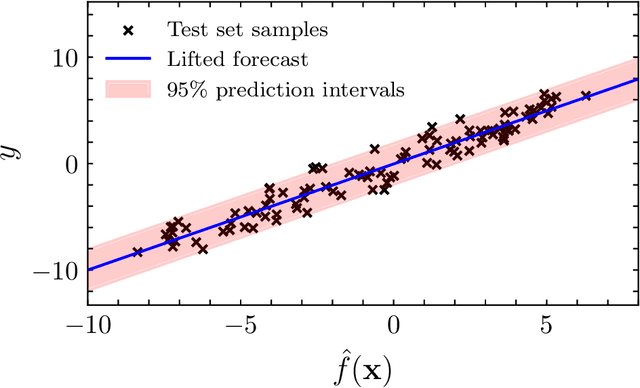
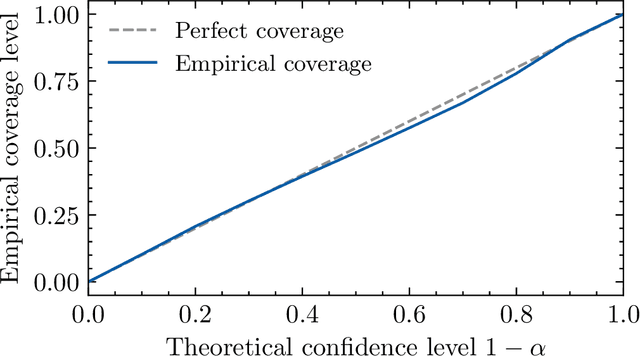
We propose the $\textit{lifted linear model}$, and derive model-free prediction intervals that become tighter as the correlation between predictions and observations increases. These intervals motivate the $\textit{Lifted Coefficient of Determination}$, a model comparison criterion for arbitrary loss functions in prediction-based settings, e.g., regression, classification or counts. We extend the prediction intervals to more general error distributions, and propose a fast model-free outlier detection algorithm for regression. Finally, we illustrate the framework via numerical experiments.

Likelihood-based inference and forecasting for trawl processes: a stochastic optimization approach

We consider trawl processes, which are stationary and infinitely divisible stochastic processes and can describe a wide range of statistical properties, such as heavy tails and long memory. In this paper, we develop the first likelihood-based methodology for the inference of real-valued trawl processes and introduce novel deterministic and probabilistic forecasting methods. Being non-Markovian, with a highly intractable likelihood function, trawl processes require the use of composite likelihood functions to parsimoniously capture their statistical properties. We formulate the composite likelihood estimation as a stochastic optimization problem for which it is feasible to implement iterative gradient descent methods. We derive novel gradient estimators with variances that are reduced by several orders of magnitude. We analyze both the theoretical properties and practical implementation details of these estimators and release a Python library which can be used to fit a large class of trawl processes. In a simulation study, we demonstrate that our estimators outperform the generalized method of moments estimators in terms of both parameter estimation error and out-of-sample forecasting error. Finally, we formalize a stochastic chain rule for our gradient estimators. We apply the new theory to trawl processes and provide a unified likelihood-based methodology for the inference of both real-valued and integer-valued trawl processes.

Stability of Multi-Agent Learning: Convergence in Network Games with Many Players

The behaviour of multi-agent learning in many player games has been shown to display complex dynamics outside of restrictive examples such as network zero-sum games. In addition, it has been shown that convergent behaviour is less likely to occur as the number of players increase. To make progress in resolving this problem, we study Q-Learning dynamics and determine a sufficient condition for the dynamics to converge to a unique equilibrium in any network game. We find that this condition depends on the nature of pairwise interactions and on the network structure, but is explicitly independent of the total number of agents in the game. We evaluate this result on a number of representative network games and show that, under suitable network conditions, stable learning dynamics can be achieved with an arbitrary number of agents.