Lifted Coefficient of Determination: Fast model-free prediction intervals and likelihood-free model comparison
Paper and Code
Oct 11, 2024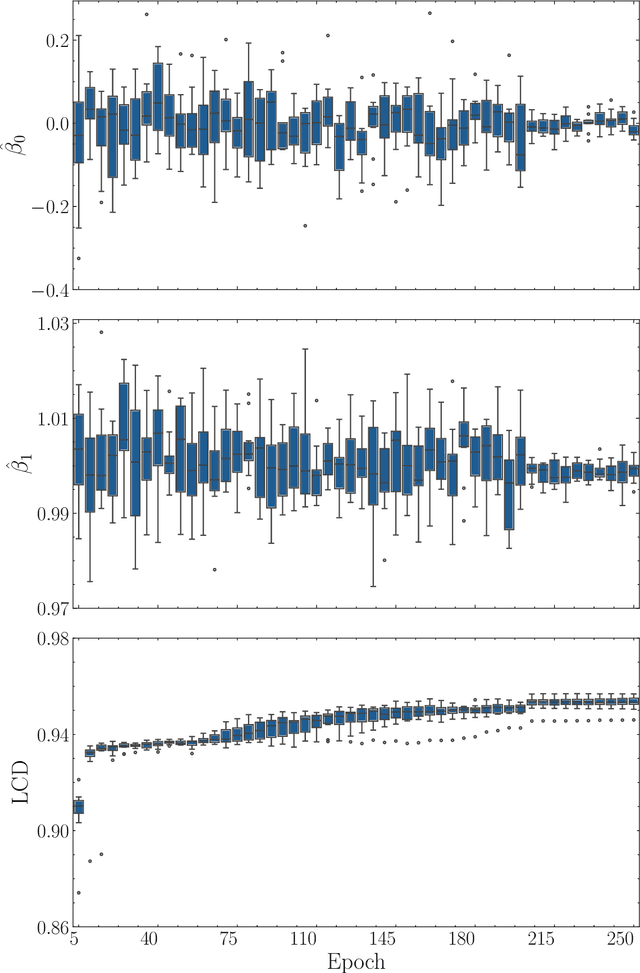
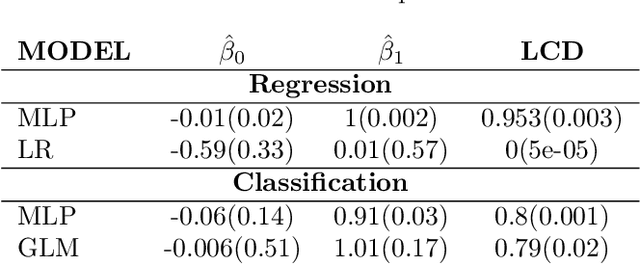
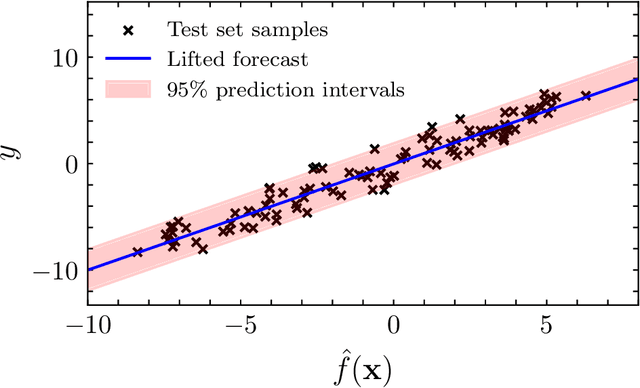
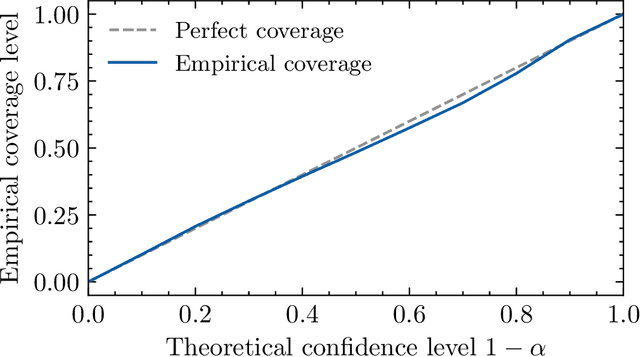
We propose the $\textit{lifted linear model}$, and derive model-free prediction intervals that become tighter as the correlation between predictions and observations increases. These intervals motivate the $\textit{Lifted Coefficient of Determination}$, a model comparison criterion for arbitrary loss functions in prediction-based settings, e.g., regression, classification or counts. We extend the prediction intervals to more general error distributions, and propose a fast model-free outlier detection algorithm for regression. Finally, we illustrate the framework via numerical experiments.
* 14 pages, 5 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge