Aamal Hussain
Light-Weight Diffusion Multiplier and Uncertainty Quantification for Fourier Neural Operators
Aug 01, 2025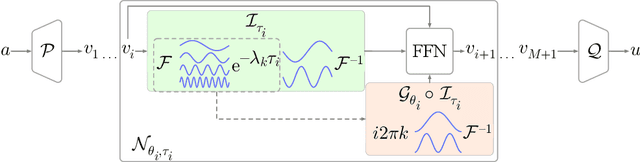
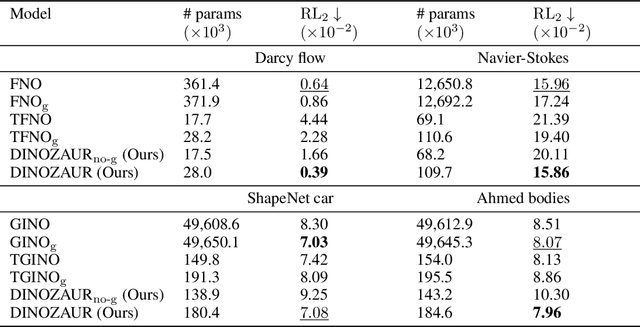
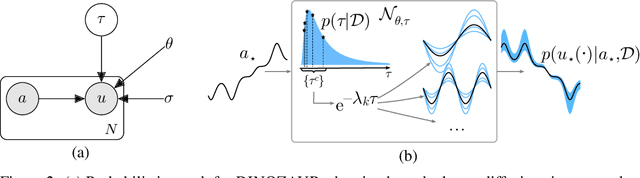
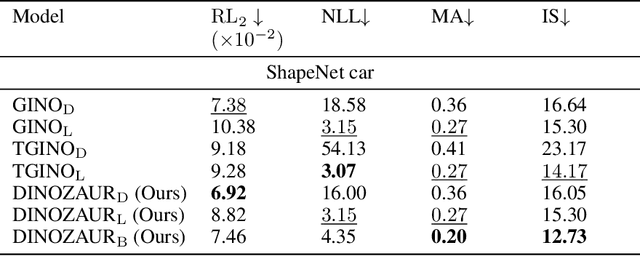
Abstract:Operator learning is a powerful paradigm for solving partial differential equations, with Fourier Neural Operators serving as a widely adopted foundation. However, FNOs face significant scalability challenges due to overparameterization and offer no native uncertainty quantification -- a key requirement for reliable scientific and engineering applications. Instead, neural operators rely on post hoc UQ methods that ignore geometric inductive biases. In this work, we introduce DINOZAUR: a diffusion-based neural operator parametrization with uncertainty quantification. Inspired by the structure of the heat kernel, DINOZAUR replaces the dense tensor multiplier in FNOs with a dimensionality-independent diffusion multiplier that has a single learnable time parameter per channel, drastically reducing parameter count and memory footprint without compromising predictive performance. By defining priors over those time parameters, we cast DINOZAUR as a Bayesian neural operator to yield spatially correlated outputs and calibrated uncertainty estimates. Our method achieves competitive or superior performance across several PDE benchmarks while providing efficient uncertainty quantification.
Multi-Agent Q-Learning Dynamics in Random Networks: Convergence due to Exploration and Sparsity
Mar 13, 2025Abstract:Beyond specific settings, many multi-agent learning algorithms fail to converge to an equilibrium solution, and instead display complex, non-stationary behaviours such as recurrent or chaotic orbits. In fact, recent literature suggests that such complex behaviours are likely to occur when the number of agents increases. In this paper, we study Q-learning dynamics in network polymatrix games where the network structure is drawn from classical random graph models. In particular, we focus on the Erdos-Renyi model, a well-studied model for social networks, and the Stochastic Block model, which generalizes the above by accounting for community structures within the network. In each setting, we establish sufficient conditions under which the agents' joint strategies converge to a unique equilibrium. We investigate how this condition depends on the exploration rates, payoff matrices and, crucially, the sparsity of the network. Finally, we validate our theoretical findings through numerical simulations and demonstrate that convergence can be reliably achieved in many-agent systems, provided network sparsity is controlled.
Stability of Multi-Agent Learning in Competitive Networks: Delaying the Onset of Chaos
Dec 19, 2023Abstract:The behaviour of multi-agent learning in competitive network games is often studied within the context of zero-sum games, in which convergence guarantees may be obtained. However, outside of this class the behaviour of learning is known to display complex behaviours and convergence cannot be always guaranteed. Nonetheless, in order to develop a complete picture of the behaviour of multi-agent learning in competitive settings, the zero-sum assumption must be lifted. Motivated by this we study the Q-Learning dynamics, a popular model of exploration and exploitation in multi-agent learning, in competitive network games. We determine how the degree of competition, exploration rate and network connectivity impact the convergence of Q-Learning. To study generic competitive games, we parameterise network games in terms of correlations between agent payoffs and study the average behaviour of the Q-Learning dynamics across all games drawn from a choice of this parameter. This statistical approach establishes choices of parameters for which Q-Learning dynamics converge to a stable fixed point. Differently to previous works, we find that the stability of Q-Learning is explicitly dependent only on the network connectivity rather than the total number of agents. Our experiments validate these findings and show that, under certain network structures, the total number of agents can be increased without increasing the likelihood of unstable or chaotic behaviours.
Stability of Multi-Agent Learning: Convergence in Network Games with Many Players
Jul 26, 2023



Abstract:The behaviour of multi-agent learning in many player games has been shown to display complex dynamics outside of restrictive examples such as network zero-sum games. In addition, it has been shown that convergent behaviour is less likely to occur as the number of players increase. To make progress in resolving this problem, we study Q-Learning dynamics and determine a sufficient condition for the dynamics to converge to a unique equilibrium in any network game. We find that this condition depends on the nature of pairwise interactions and on the network structure, but is explicitly independent of the total number of agents in the game. We evaluate this result on a number of representative network games and show that, under suitable network conditions, stable learning dynamics can be achieved with an arbitrary number of agents.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge