Damien Woods
Turning machines
Sep 02, 2020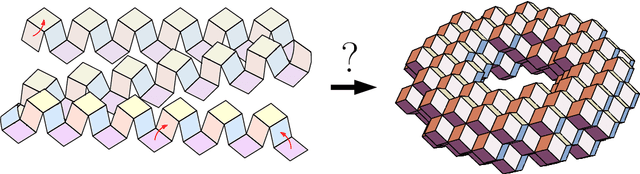
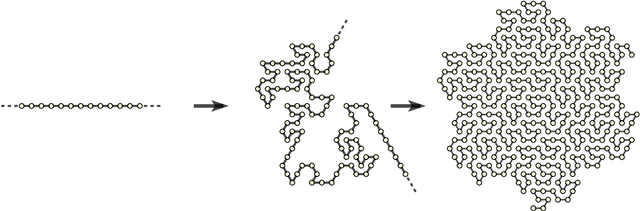
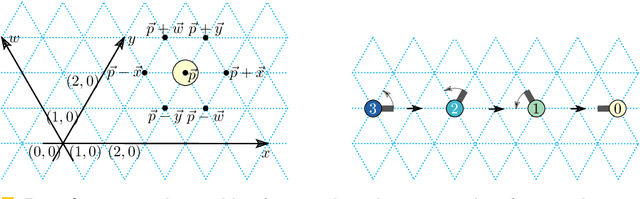
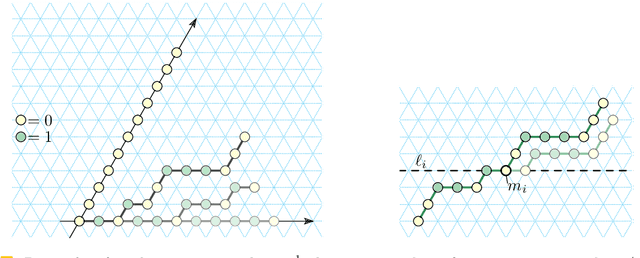
Abstract:Molecular robotics is challenging, so it seems best to keep it simple. We consider an abstract molecular robotics model based on simple folding instructions that execute asynchronously. Turning Machines are a simple 1D to 2D folding model, also easily generalisable to 2D to 3D folding. A Turning Machine starts out as a line of connected monomers in the discrete plane, each with an associated turning number. A monomer turns relative to its neighbours, executing a unit-distance translation that drags other monomers along with it, and through collective motion the initial set of monomers eventually folds into a programmed shape. We fully characterise the ability of Turning Machines to execute line rotations, and to do so efficiently: computing an almost-full line rotation of $5\pi/3$ radians is possible, yet a full $2\pi$ rotation is impossible. We show that such line-rotations represent a fundamental primitive in the model, by using them to efficiently and asynchronously fold arbitrarily large zig-zag-rastered squares and $y$-monotone shapes.
Parallel computation using active self-assembly
Sep 05, 2014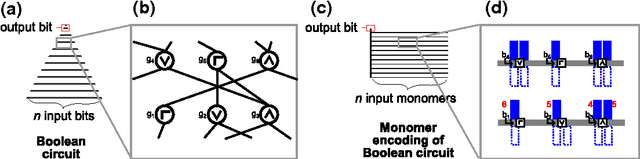

Abstract:We study the computational complexity of the recently proposed nubot model of molecular-scale self-assembly. The model generalises asynchronous cellular automata to have non-local movement where large assemblies of molecules can be pushed and pulled around, analogous to millions of molecular motors in animal muscle effecting the rapid movement of macroscale arms and legs. We show that the nubot model is capable of simulating Boolean circuits of polylogarithmic depth and polynomial size, in only polylogarithmic expected time. In computational complexity terms, we show that any problem from the complexity class NC is solvable in polylogarithmic expected time and polynomial workspace using nubots. Along the way, we give fast parallel nubot algorithms for a number of problems including line growth, sorting, Boolean matrix multiplication and space-bounded Turing machine simulation, all using a constant number of nubot states (monomer types). Circuit depth is a well-studied notion of parallel time, and our result implies that the nubot model is a highly parallel model of computation in a formal sense. Asynchronous cellular automata are not capable of this parallelism, and our result shows that adding a rigid-body movement primitive to such a model, to get the nubot model, drastically increases parallel processing abilities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge