Cai Wood
Turning machines
Sep 02, 2020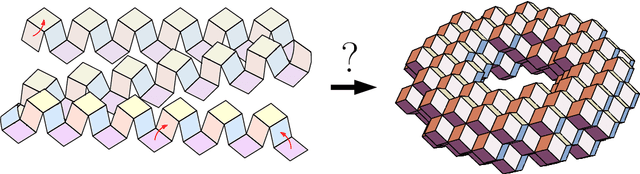
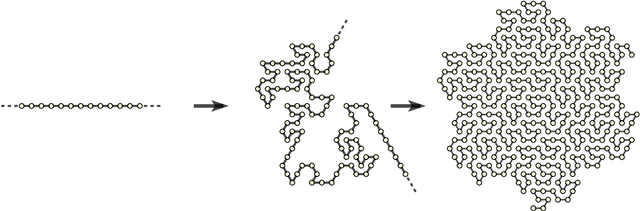
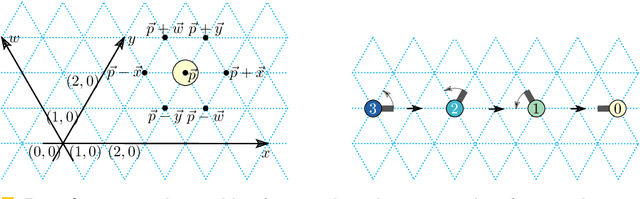
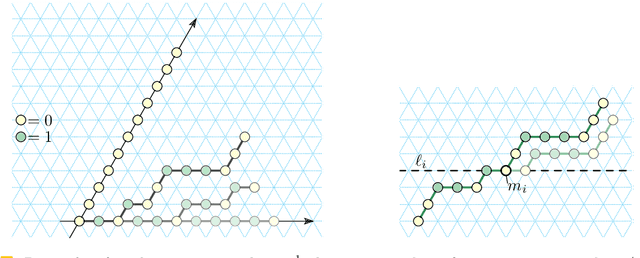
Abstract:Molecular robotics is challenging, so it seems best to keep it simple. We consider an abstract molecular robotics model based on simple folding instructions that execute asynchronously. Turning Machines are a simple 1D to 2D folding model, also easily generalisable to 2D to 3D folding. A Turning Machine starts out as a line of connected monomers in the discrete plane, each with an associated turning number. A monomer turns relative to its neighbours, executing a unit-distance translation that drags other monomers along with it, and through collective motion the initial set of monomers eventually folds into a programmed shape. We fully characterise the ability of Turning Machines to execute line rotations, and to do so efficiently: computing an almost-full line rotation of $5\pi/3$ radians is possible, yet a full $2\pi$ rotation is impossible. We show that such line-rotations represent a fundamental primitive in the model, by using them to efficiently and asynchronously fold arbitrarily large zig-zag-rastered squares and $y$-monotone shapes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge