Parallel computation using active self-assembly
Paper and Code
Sep 05, 2014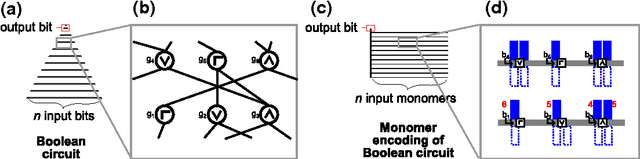
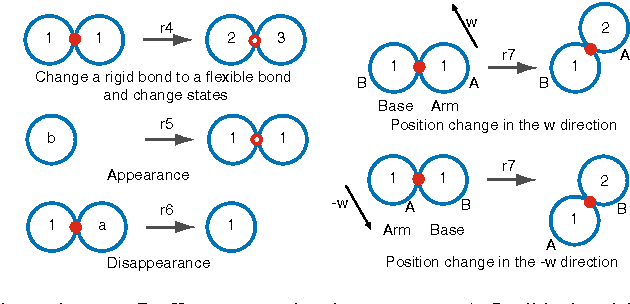

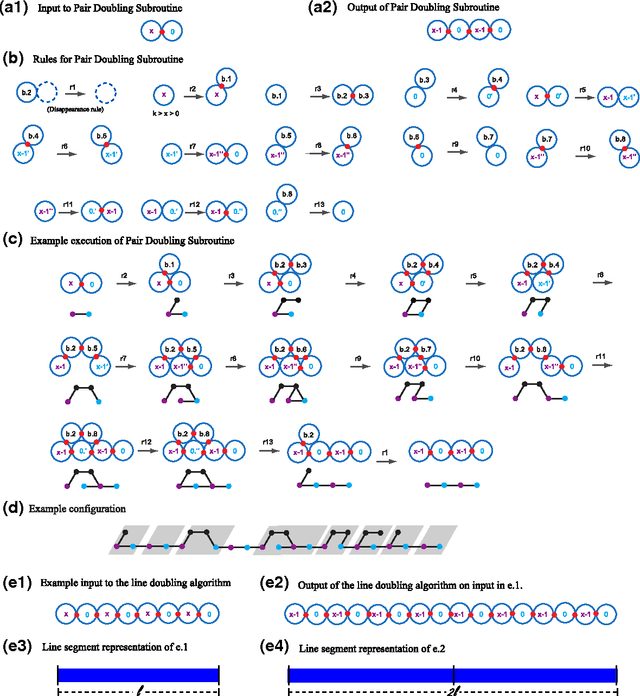
We study the computational complexity of the recently proposed nubot model of molecular-scale self-assembly. The model generalises asynchronous cellular automata to have non-local movement where large assemblies of molecules can be pushed and pulled around, analogous to millions of molecular motors in animal muscle effecting the rapid movement of macroscale arms and legs. We show that the nubot model is capable of simulating Boolean circuits of polylogarithmic depth and polynomial size, in only polylogarithmic expected time. In computational complexity terms, we show that any problem from the complexity class NC is solvable in polylogarithmic expected time and polynomial workspace using nubots. Along the way, we give fast parallel nubot algorithms for a number of problems including line growth, sorting, Boolean matrix multiplication and space-bounded Turing machine simulation, all using a constant number of nubot states (monomer types). Circuit depth is a well-studied notion of parallel time, and our result implies that the nubot model is a highly parallel model of computation in a formal sense. Asynchronous cellular automata are not capable of this parallelism, and our result shows that adding a rigid-body movement primitive to such a model, to get the nubot model, drastically increases parallel processing abilities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge