On Uniform Convergence and Low-Norm Interpolation Learning

We consider an underdetermined noisy linear regression model where the minimum-norm interpolating predictor is known to be consistent, and ask: can uniform convergence in a norm ball, or at least (following Nagarajan and Kolter) the subset of a norm ball that the algorithm selects on a typical input set, explain this success? We show that uniformly bounding the difference between empirical and population errors cannot show any learning in the norm ball, and cannot show consistency for any set, even one depending on the exact algorithm and distribution. But we argue we can explain the consistency of the minimal-norm interpolator with a slightly weaker, yet standard, notion, uniform convergence of zero-error predictors. We use this to bound the generalization error of low- (but not minimal-) norm interpolating predictors.

Learning Deep Kernels for Non-Parametric Two-Sample Tests

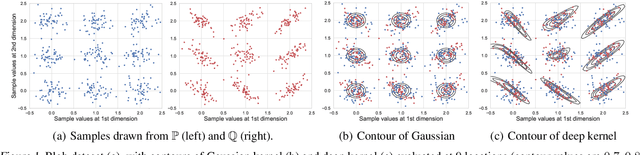
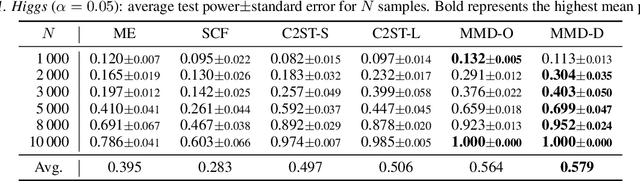
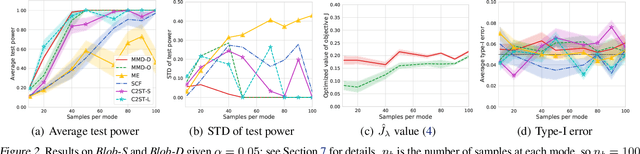
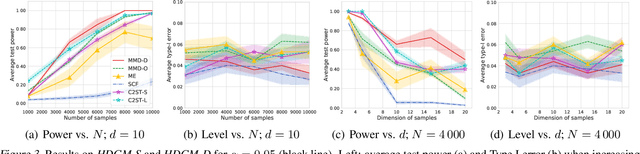
We propose a class of kernel-based two-sample tests, which aim to determine whether two sets of samples are drawn from the same distribution. Our tests are constructed from kernels parameterized by deep neural nets, trained to maximize test power. These tests adapt to variations in distribution smoothness and shape over space, and are especially suited to high dimensions and complex data. By contrast, the simpler kernels used in prior kernel testing work are spatially homogeneous, and adaptive only in lengthscale. We explain how this scheme includes popular classifier-based two-sample tests as a special case, but improves on them in general. We provide the first proof of consistency for the proposed adaptation method, which applies both to kernels on deep features and to simpler radial basis kernels or multiple kernel learning. In experiments, we establish the superior performance of our deep kernels in hypothesis testing on benchmark and real-world data. The code of our deep-kernel-based two sample tests is available at https://github.com/fengliu90/DK-for-TST.