Deep Dynamic Factor Models

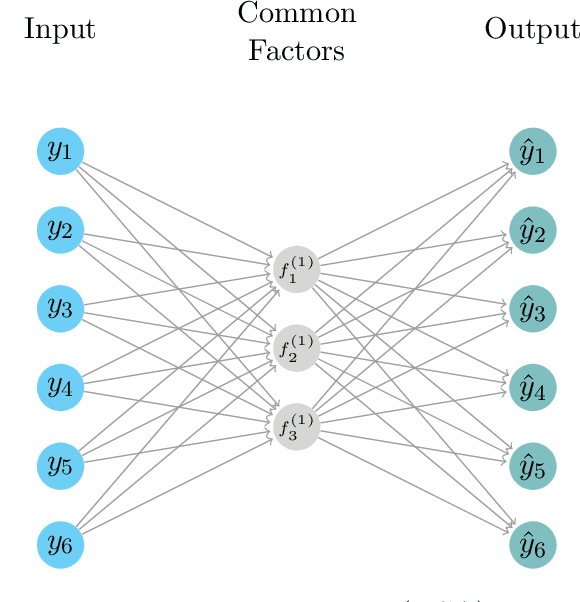
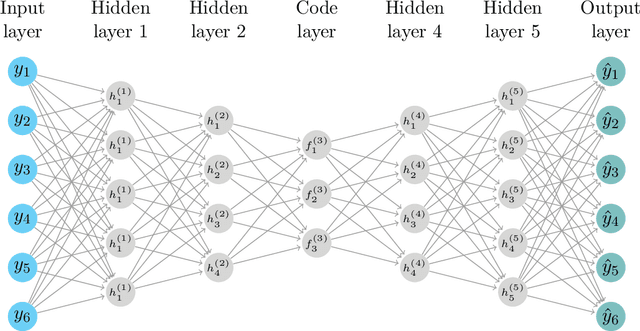
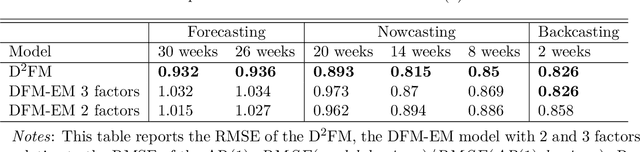
We propose a novel deep neural net framework - that we refer to as Deep Dynamic Factor Model (D2FM) -, to encode the information available, from hundreds of macroeconomic and financial time-series into a handful of unobserved latent states. While similar in spirit to traditional dynamic factor models (DFMs), differently from those, this new class of models allows for nonlinearities between factors and observables due to the deep neural net structure. However, by design, the latent states of the model can still be interpreted as in a standard factor model. In an empirical application to the forecast and nowcast of economic conditions in the US, we show the potential of this framework in dealing with high dimensional, mixed frequencies and asynchronously published time series data. In a fully real-time out-of-sample exercise with US data, the D2FM improves over the performances of a state-of-the-art DFM.

A Baseline for Shapley Values in MLPs: from Missingness to Neutrality

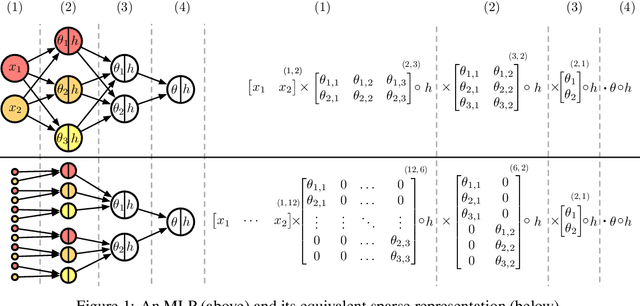
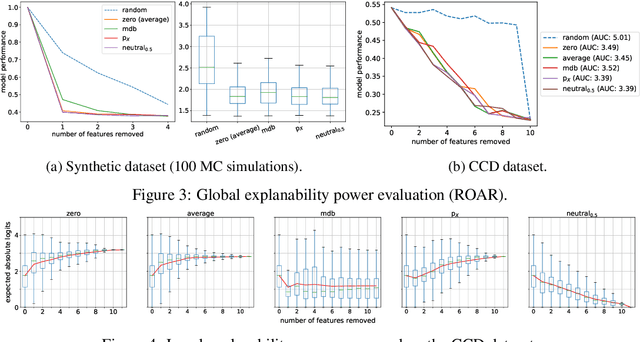
Being able to explain a prediction as well as having a model that performs well are paramount in many machine learning applications. Deep neural networks have gained momentum recently on the basis of their accuracy, however these are often criticised to be black-boxes. Many authors have focused on proposing methods to explain their predictions. Among these explainability methods, feature attribution methods have been favoured for their strong theoretical foundation: the Shapley value. A limitation of Shapley value is the need to define a baseline (aka reference point) representing the missingness of a feature. In this paper, we present a method to choose a baseline based on a neutrality value: a parameter defined by decision makers at which their choices are determined by the returned value of the model being either below or above it. Based on this concept, we theoretically justify these neutral baselines and find a way to identify them for MLPs. Then, we experimentally demonstrate that for a binary classification task, using a synthetic dataset and a dataset coming from the financial domain, the proposed baselines outperform, in terms of local explanability power, standard ways of choosing them.

Explaining a prediction in some nonlinear models

In this article we will analyse how to compute the contribution of each input value to its aggregate output in some nonlinear models. Regression and classification applications, together with related algorithms for deep neural networks are presented. The proposed approach merges two methods currently present in the literature: integrated gradient and deep Taylor decomposition.