Dr. KID: Direct Remeshing and K-set Isometric Decomposition for Scalable Physicalization of Organic Shapes

Dr. KID is an algorithm that uses isometric decomposition for the physicalization of potato-shaped organic models in a puzzle fashion. The algorithm begins with creating a simple, regular triangular surface mesh of organic shapes, followed by iterative k-means clustering and remeshing. For clustering, we need similarity between triangles (segments) which is defined as a distance function. The distance function maps each triangle's shape to a single point in the virtual 3D space. Thus, the distance between the triangles indicates their degree of dissimilarity. K-means clustering uses this distance and sorts of segments into k classes. After this, remeshing is applied to minimize the distance between triangles within the same cluster by making their shapes identical. Clustering and remeshing are repeated until the distance between triangles in the same cluster reaches an acceptable threshold. We adopt a curvature-aware strategy to determine the surface thickness and finalize puzzle pieces for 3D printing. Identical hinges and holes are created for assembling the puzzle components. For smoother outcomes, we use triangle subdivision along with curvature-aware clustering, generating curved triangular patches for 3D printing. Our algorithm was evaluated using various models, and the 3D-printed results were analyzed. Findings indicate that our algorithm performs reliably on target organic shapes with minimal loss of input geometry.

Differentiable Electron Microscopy Simulation: Methods and Applications for Visualization

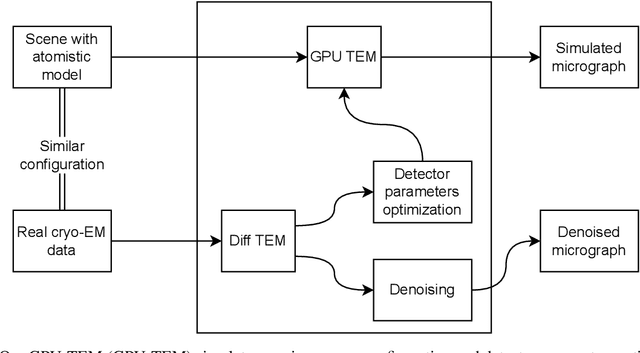
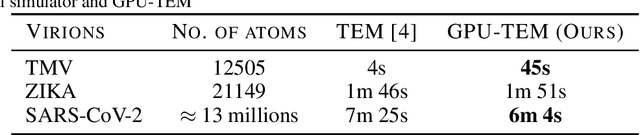
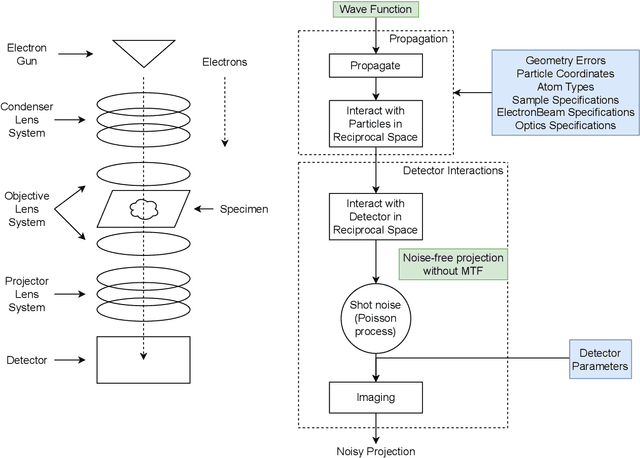
We propose a new microscopy simulation system that can depict atomistic models in a micrograph visual style, similar to results of physical electron microscopy imaging. This system is scalable, able to represent simulation of electron microscopy of tens of viral particles and synthesizes the image faster than previous methods. On top of that, the simulator is differentiable, both its deterministic as well as stochastic stages that form signal and noise representations in the micrograph. This notable property has the capability for solving inverse problems by means of optimization and thus allows for generation of microscopy simulations using the parameter settings estimated from real data. We demonstrate this learning capability through two applications: (1) estimating the parameters of the modulation transfer function defining the detector properties of the simulated and real micrographs, and (2) denoising the real data based on parameters trained from the simulated examples. While current simulators do not support any parameter estimation due to their forward design, we show that the results obtained using estimated parameters are very similar to the results of real micrographs. Additionally, we evaluate the denoising capabilities of our approach and show that the results showed an improvement over state-of-the-art methods. Denoised micrographs exhibit less noise in the tilt-series tomography reconstructions, ultimately reducing the visual dominance of noise in direct volume rendering of microscopy tomograms.