Outbidding and Outbluffing Elite Humans: Mastering Liar's Poker via Self-Play and Reinforcement Learning

AI researchers have long focused on poker-like games as a testbed for environments characterized by multi-player dynamics, imperfect information, and reasoning under uncertainty. While recent breakthroughs have matched elite human play at no-limit Texas hold'em, the multi-player dynamics are subdued: most hands converge quickly with only two players engaged through multiple rounds of bidding. In this paper, we present Solly, the first AI agent to achieve elite human play in reduced-format Liar's Poker, a game characterized by extensive multi-player engagement. We trained Solly using self-play with a model-free, actor-critic, deep reinforcement learning algorithm. Solly played at an elite human level as measured by win rate (won over 50% of hands) and equity (money won) in heads-up and multi-player Liar's Poker. Solly also outperformed large language models (LLMs), including those with reasoning abilities, on the same metrics. Solly developed novel bidding strategies, randomized play effectively, and was not easily exploitable by world-class human players.

Optimal Dynamic Fees for Blockchain Resources

We develop a general and practical framework to address the problem of the optimal design of dynamic fee mechanisms for multiple blockchain resources. Our framework allows to compute policies that optimally trade-off between adjusting resource prices to handle persistent demand shifts versus being robust to local noise in the observed block demand. In the general case with more than one resource, our optimal policies correctly handle cross-effects (complementarity and substitutability) in resource demands. We also show how these cross-effects can be used to inform resource design, i.e. combining resources into bundles that have low demand-side cross-effects can yield simpler and more efficient price-update rules. Our framework is also practical, we demonstrate how it can be used to refine or inform the design of heuristic fee update rules such as EIP-1559 or EIP-4844 with two case studies. We then estimate a uni-dimensional version of our model using real market data from the Ethereum blockchain and empirically compare the performance of our optimal policies to EIP-1559.

Policy Gradient Optimization of Thompson Sampling Policies

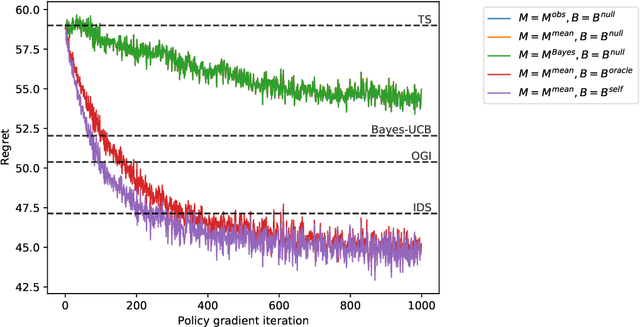
We study the use of policy gradient algorithms to optimize over a class of generalized Thompson sampling policies. Our central insight is to view the posterior parameter sampled by Thompson sampling as a kind of pseudo-action. Policy gradient methods can then be tractably applied to search over a class of sampling policies, which determine a probability distribution over pseudo-actions (i.e., sampled parameters) as a function of observed data. We also propose and compare policy gradient estimators that are specialized to Bayesian bandit problems. Numerical experiments demonstrate that direct policy search on top of Thompson sampling automatically corrects for some of the algorithm's known shortcomings and offers meaningful improvements even in long horizon problems where standard Thompson sampling is extremely effective.

Thompson Sampling with Information Relaxation Penalties

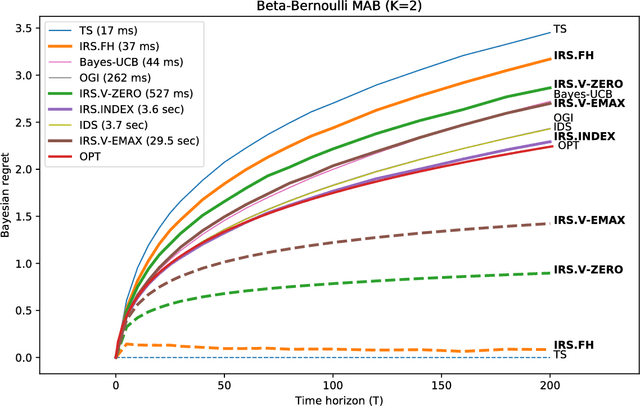
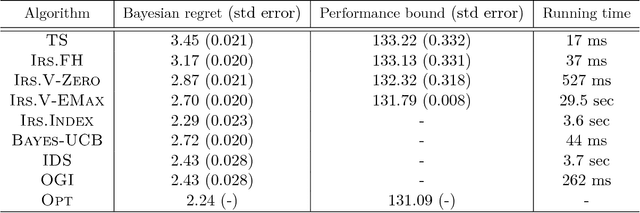
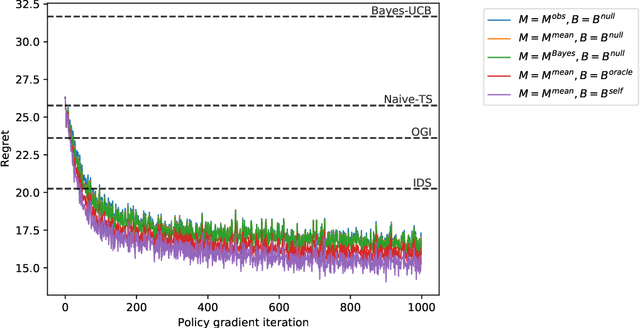
We consider a finite time horizon multi-armed bandit (MAB) problem in a Bayesian framework, for which we develop a general set of control policies that leverage ideas from information relaxations of stochastic dynamic optimization problems. In crude terms, an information relaxation allows the decision maker (DM) to have access to the future (unknown) rewards and incorporate them in her optimization problem to pick an action at time $t$, but penalizes the decision maker for using this information. In our setting, the future rewards allow the DM to better estimate the unknown mean reward parameters of the multiple arms, and optimize her sequence of actions. By picking different information penalties, the DM can construct a family of policies of increasing complexity that, for example, include Thompson Sampling and the true optimal (but intractable) policy as special cases. We systematically develop this framework of information relaxation sampling, propose an intuitive family of control policies for our motivating finite time horizon Bayesian MAB problem, and prove associated structural results and performance bounds. Numerical experiments suggest that this new class of policies performs well, in particular in settings where the finite time horizon introduces significant tension in the problem. Finally, inspired by the finite time horizon Gittins index, we propose an index policy that builds on our framework that particularly outperforms to the state-of-the-art algorithms in our numerical experiments.

Universal Reinforcement Learning

We consider an agent interacting with an unmodeled environment. At each time, the agent makes an observation, takes an action, and incurs a cost. Its actions can influence future observations and costs. The goal is to minimize the long-term average cost. We propose a novel algorithm, known as the active LZ algorithm, for optimal control based on ideas from the Lempel-Ziv scheme for universal data compression and prediction. We establish that, under the active LZ algorithm, if there exists an integer $K$ such that the future is conditionally independent of the past given a window of $K$ consecutive actions and observations, then the average cost converges to the optimum. Experimental results involving the game of Rock-Paper-Scissors illustrate merits of the algorithm.

Convergence of Min-Sum Message Passing for Quadratic Optimization

We establish the convergence of the min-sum message passing algorithm for minimization of a broad class of quadratic objective functions: those that admit a convex decomposition. Our results also apply to the equivalent problem of the convergence of Gaussian belief propagation.

Consensus Propagation

We propose consensus propagation, an asynchronous distributed protocol for averaging numbers across a network. We establish convergence, characterize the convergence rate for regular graphs, and demonstrate that the protocol exhibits better scaling properties than pairwise averaging, an alternative that has received much recent attention. Consensus propagation can be viewed as a special case of belief propagation, and our results contribute to the belief propagation literature. In particular, beyond singly-connected graphs, there are very few classes of relevant problems for which belief propagation is known to converge.