On the Optimality of Tracking Fisher Information in Adaptive Testing with Stochastic Binary Responses

We study the problem of estimating a continuous ability parameter from sequential binary responses by actively asking questions with varying difficulties, a setting that arises naturally in adaptive testing and online preference learning. Our goal is to certify that the estimate lies within a desired margin of error, using as few queries as possible. We propose a simple algorithm that adaptively selects questions to maximize Fisher information and updates the estimate using a method-of-moments approach, paired with a novel test statistic to decide when the estimate is accurate enough. We prove that this Fisher-tracking strategy achieves optimal performance in both fixed-confidence and fixed-budget regimes, which are commonly invested in the best-arm identification literature. Our analysis overcomes a key technical challenge in the fixed-budget setting -- handling the dependence between the evolving estimate and the query distribution -- by exploiting a structural symmetry in the model and combining large deviation tools with Ville's inequality. Our results provide rigorous theoretical support for simple and efficient adaptive testing procedures.

Improving Thompson Sampling via Information Relaxation for Budgeted Multi-armed Bandits

We consider a Bayesian budgeted multi-armed bandit problem, in which each arm consumes a different amount of resources when selected and there is a budget constraint on the total amount of resources that can be used. Budgeted Thompson Sampling (BTS) offers a very effective heuristic to this problem, but its arm-selection rule does not take into account the remaining budget information. We adopt \textit{Information Relaxation Sampling} framework that generalizes Thompson Sampling for classical $K$-armed bandit problems, and propose a series of algorithms that are randomized like BTS but more carefully optimize their decisions with respect to the budget constraint. In a one-to-one correspondence with these algorithms, a series of performance benchmarks that improve the conventional benchmark are also suggested. Our theoretical analysis and simulation results show that our algorithms (and our benchmarks) make incremental improvements over BTS (respectively, the conventional benchmark) across various settings including a real-world example.

An Information-Theoretic Analysis of Nonstationary Bandit Learning

In nonstationary bandit learning problems, the decision-maker must continually gather information and adapt their action selection as the latent state of the environment evolves. In each time period, some latent optimal action maximizes expected reward under the environment state. We view the optimal action sequence as a stochastic process, and take an information-theoretic approach to analyze attainable performance. We bound limiting per-period regret in terms of the entropy rate of the optimal action process. The bound applies to a wide array of problems studied in the literature and reflects the problem's information structure through its information-ratio.

Policy Gradient Optimization of Thompson Sampling Policies

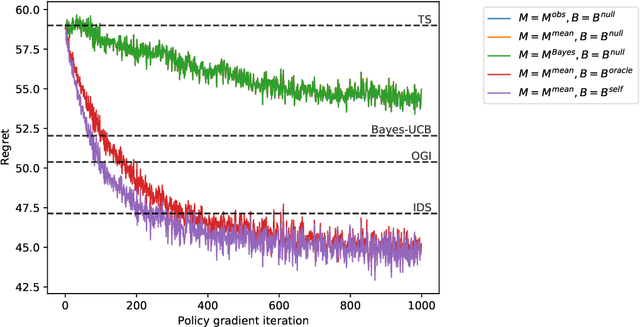
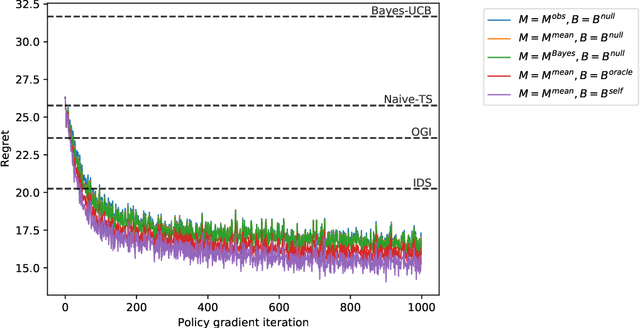
We study the use of policy gradient algorithms to optimize over a class of generalized Thompson sampling policies. Our central insight is to view the posterior parameter sampled by Thompson sampling as a kind of pseudo-action. Policy gradient methods can then be tractably applied to search over a class of sampling policies, which determine a probability distribution over pseudo-actions (i.e., sampled parameters) as a function of observed data. We also propose and compare policy gradient estimators that are specialized to Bayesian bandit problems. Numerical experiments demonstrate that direct policy search on top of Thompson sampling automatically corrects for some of the algorithm's known shortcomings and offers meaningful improvements even in long horizon problems where standard Thompson sampling is extremely effective.

Thompson Sampling with Information Relaxation Penalties

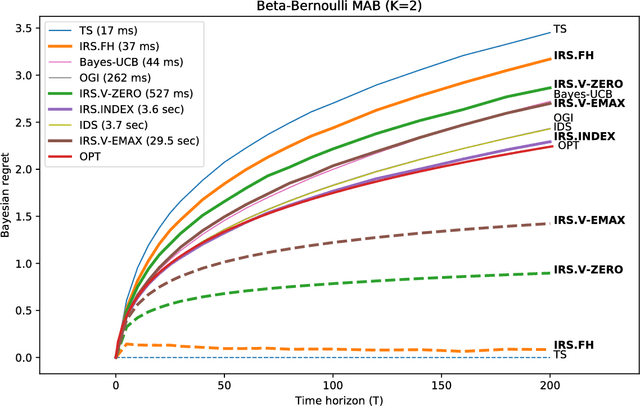
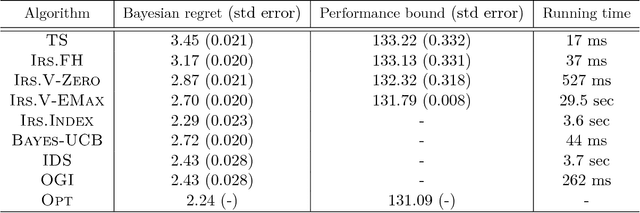
We consider a finite time horizon multi-armed bandit (MAB) problem in a Bayesian framework, for which we develop a general set of control policies that leverage ideas from information relaxations of stochastic dynamic optimization problems. In crude terms, an information relaxation allows the decision maker (DM) to have access to the future (unknown) rewards and incorporate them in her optimization problem to pick an action at time $t$, but penalizes the decision maker for using this information. In our setting, the future rewards allow the DM to better estimate the unknown mean reward parameters of the multiple arms, and optimize her sequence of actions. By picking different information penalties, the DM can construct a family of policies of increasing complexity that, for example, include Thompson Sampling and the true optimal (but intractable) policy as special cases. We systematically develop this framework of information relaxation sampling, propose an intuitive family of control policies for our motivating finite time horizon Bayesian MAB problem, and prove associated structural results and performance bounds. Numerical experiments suggest that this new class of policies performs well, in particular in settings where the finite time horizon introduces significant tension in the problem. Finally, inspired by the finite time horizon Gittins index, we propose an index policy that builds on our framework that particularly outperforms to the state-of-the-art algorithms in our numerical experiments.