Archetypal Graph Generative Models: Explainable and Identifiable Communities via Anchor-Dominant Convex Hulls

Representation learning has been essential for graph machine learning tasks such as link prediction, community detection, and network visualization. Despite recent advances in achieving high performance on these downstream tasks, little progress has been made toward self-explainable models. Understanding the patterns behind predictions is equally important, motivating recent interest in explainable machine learning. In this paper, we present GraphHull, an explainable generative model that represents networks using two levels of convex hulls. At the global level, the vertices of a convex hull are treated as archetypes, each corresponding to a pure community in the network. At the local level, each community is refined by a prototypical hull whose vertices act as representative profiles, capturing community-specific variation. This two-level construction yields clear multi-scale explanations: a node's position relative to global archetypes and its local prototypes directly accounts for its edges. The geometry is well-behaved by design, while local hulls are kept disjoint by construction. To further encourage diversity and stability, we place principled priors, including determinantal point processes, and fit the model under MAP estimation with scalable subsampling. Experiments on real networks demonstrate the ability of GraphHull to recover multi-level community structure and to achieve competitive or superior performance in link prediction and community detection, while naturally providing interpretable predictions.

The Signed Two-Space Proximity Model for Learning Representations in Protein-Protein Interaction Networks

Accurately predicting complex protein-protein interactions (PPIs) is crucial for decoding biological processes, from cellular functioning to disease mechanisms. However, experimental methods for determining PPIs are computationally expensive. Thus, attention has been recently drawn to machine learning approaches. Furthermore, insufficient effort has been made toward analyzing signed PPI networks, which capture both activating (positive) and inhibitory (negative) interactions. To accurately represent biological relationships, we present the Signed Two-Space Proximity Model (S2-SPM) for signed PPI networks, which explicitly incorporates both types of interactions, reflecting the complex regulatory mechanisms within biological systems. This is achieved by leveraging two independent latent spaces to differentiate between positive and negative interactions while representing protein similarity through proximity in these spaces. Our approach also enables the identification of archetypes representing extreme protein profiles. S2-SPM's superior performance in predicting the presence and sign of interactions in SPPI networks is demonstrated in link prediction tasks against relevant baseline methods. Additionally, the biological prevalence of the identified archetypes is confirmed by an enrichment analysis of Gene Ontology (GO) terms, which reveals that distinct biological tasks are associated with archetypal groups formed by both interactions. This study is also validated regarding statistical significance and sensitivity analysis, providing insights into the functional roles of different interaction types. Finally, the robustness and consistency of the extracted archetype structures are confirmed using the Bayesian Normalized Mutual Information (BNMI) metric, proving the model's reliability in capturing meaningful SPPI patterns.

Signed Graph Autoencoder for Explainable and Polarization-Aware Network Embeddings

Autoencoders based on Graph Neural Networks (GNNs) have garnered significant attention in recent years for their ability to extract informative latent representations, characterizing the structure of complex topologies, such as graphs. Despite the prevalence of Graph Autoencoders, there has been limited focus on developing and evaluating explainable neural-based graph generative models specifically designed for signed networks. To address this gap, we propose the Signed Graph Archetypal Autoencoder (SGAAE) framework. SGAAE extracts node-level representations that express node memberships over distinct extreme profiles, referred to as archetypes, within the network. This is achieved by projecting the graph onto a learned polytope, which governs its polarization. The framework employs a recently proposed likelihood for analyzing signed networks based on the Skellam distribution, combined with relational archetypal analysis and GNNs. Our experimental evaluation demonstrates the SGAAEs' capability to successfully infer node memberships over the different underlying latent structures while extracting competing communities formed through the participation of the opposing views in the network. Additionally, we introduce the 2-level network polarization problem and show how SGAAE is able to characterize such a setting. The proposed model achieves high performance in different tasks of signed link prediction across four real-world datasets, outperforming several baseline models.

Time-Parameterized Convolutional Neural Networks for Irregularly Sampled Time Series

Irregularly sampled multivariate time series are ubiquitous in several application domains, leading to sparse, not fully-observed and non-aligned observations across different variables. Standard sequential neural network architectures, such as recurrent neural networks (RNNs) and convolutional neural networks (CNNs), consider regular spacing between observation times, posing significant challenges to irregular time series modeling. While most of the proposed architectures incorporate RNN variants to handle irregular time intervals, convolutional neural networks have not been adequately studied in the irregular sampling setting. In this paper, we parameterize convolutional layers by employing time-explicitly initialized kernels. Such general functions of time enhance the learning process of continuous-time hidden dynamics and can be efficiently incorporated into convolutional kernel weights. We, thus, propose the time-parameterized convolutional neural network (TPCNN), which shares similar properties with vanilla convolutions but is carefully designed for irregularly sampled time series. We evaluate TPCNN on both interpolation and classification tasks involving real-world irregularly sampled multivariate time series datasets. Our experimental results indicate the competitive performance of the proposed TPCNN model which is also significantly more efficient than other state-of-the-art methods. At the same time, the proposed architecture allows the interpretability of the input series by leveraging the combination of learnable time functions that improve the network performance in subsequent tasks and expedite the inaugural application of convolutions in this field.

TimeGNN: Temporal Dynamic Graph Learning for Time Series Forecasting

Time series forecasting lies at the core of important real-world applications in many fields of science and engineering. The abundance of large time series datasets that consist of complex patterns and long-term dependencies has led to the development of various neural network architectures. Graph neural network approaches, which jointly learn a graph structure based on the correlation of raw values of multivariate time series while forecasting, have recently seen great success. However, such solutions are often costly to train and difficult to scale. In this paper, we propose TimeGNN, a method that learns dynamic temporal graph representations that can capture the evolution of inter-series patterns along with the correlations of multiple series. TimeGNN achieves inference times 4 to 80 times faster than other state-of-the-art graph-based methods while achieving comparable forecasting performance

Time Series Forecasting Models Copy the Past: How to Mitigate

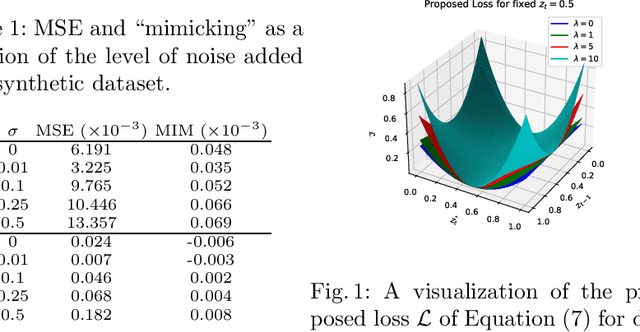
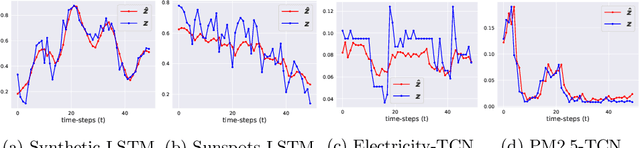
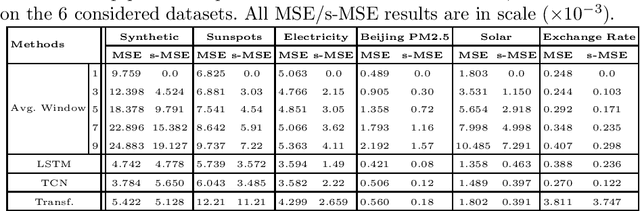
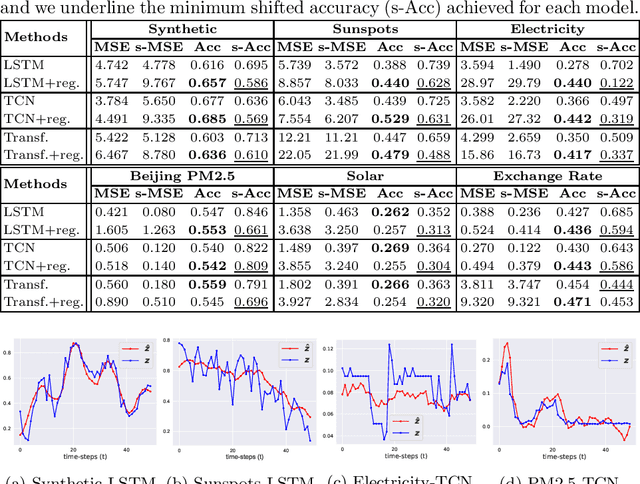
Time series forecasting is at the core of important application domains posing significant challenges to machine learning algorithms. Recently neural network architectures have been widely applied to the problem of time series forecasting. Most of these models are trained by minimizing a loss function that measures predictions' deviation from the real values. Typical loss functions include mean squared error (MSE) and mean absolute error (MAE). In the presence of noise and uncertainty, neural network models tend to replicate the last observed value of the time series, thus limiting their applicability to real-world data. In this paper, we provide a formal definition of the above problem and we also give some examples of forecasts where the problem is observed. We also propose a regularization term penalizing the replication of previously seen values. We evaluate the proposed regularization term both on synthetic and real-world datasets. Our results indicate that the regularization term mitigates to some extent the aforementioned problem and gives rise to more robust models.