Time Series Forecasting Models Copy the Past: How to Mitigate
Paper and Code
Jul 27, 2022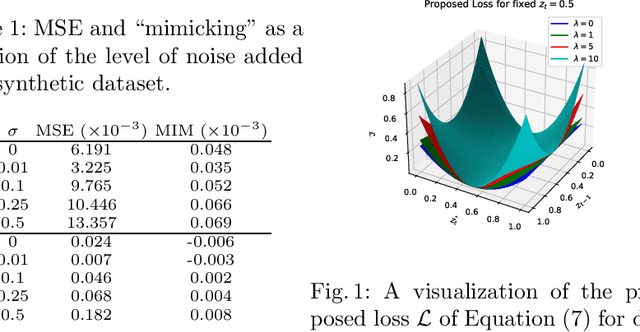
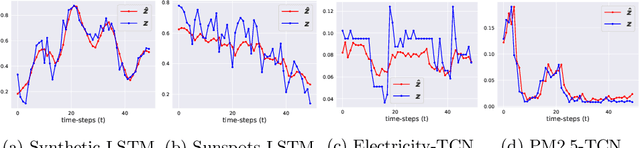
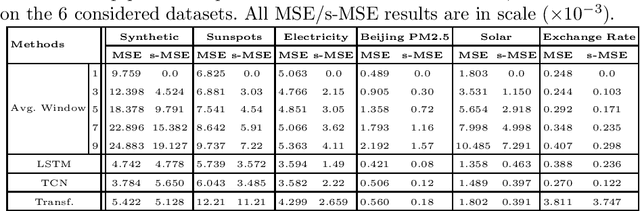
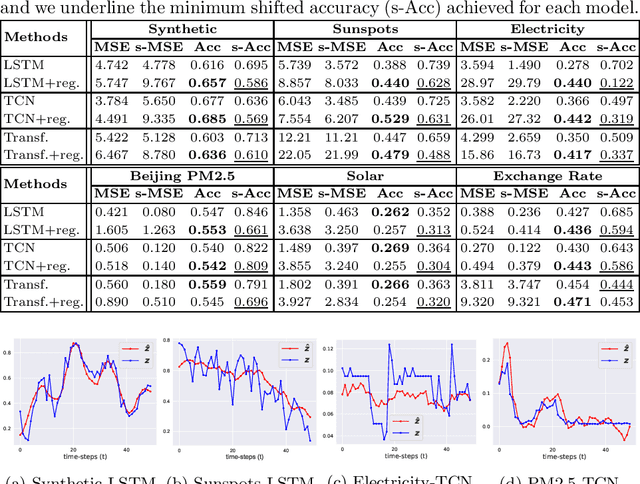
Time series forecasting is at the core of important application domains posing significant challenges to machine learning algorithms. Recently neural network architectures have been widely applied to the problem of time series forecasting. Most of these models are trained by minimizing a loss function that measures predictions' deviation from the real values. Typical loss functions include mean squared error (MSE) and mean absolute error (MAE). In the presence of noise and uncertainty, neural network models tend to replicate the last observed value of the time series, thus limiting their applicability to real-world data. In this paper, we provide a formal definition of the above problem and we also give some examples of forecasts where the problem is observed. We also propose a regularization term penalizing the replication of previously seen values. We evaluate the proposed regularization term both on synthetic and real-world datasets. Our results indicate that the regularization term mitigates to some extent the aforementioned problem and gives rise to more robust models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge