Variational Inference for Neyman-Scott Processes

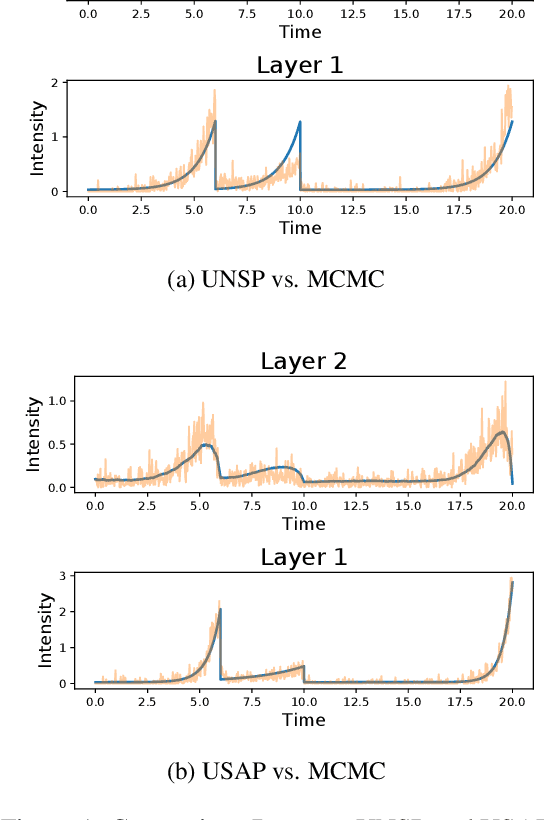
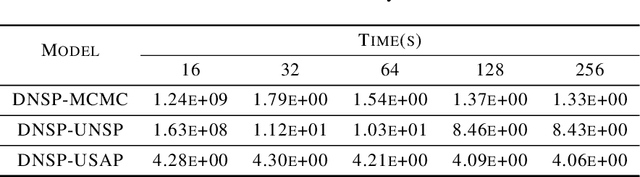
Neyman-Scott processes (NSPs) have been applied across a range of fields to model points or temporal events with a hierarchy of clusters. Markov chain Monte Carlo (MCMC) is typically used for posterior sampling in the model. However, MCMC's mixing time can cause the resulting inference to be slow, and thereby slow down model learning and prediction. We develop the first variational inference (VI) algorithm for NSPs, and give two examples of suitable variational posterior point process distributions. Our method minimizes the inclusive Kullback-Leibler (KL) divergence for VI to obtain the variational parameters. We generate samples from the approximate posterior point processes much faster than MCMC, as we can directly estimate the approximate posterior point processes without any MCMC steps or gradient descent. We include synthetic and real-world data experiments that demonstrate our VI algorithm achieves better prediction performance than MCMC when computational time is limited.

Deep Neyman-Scott Processes

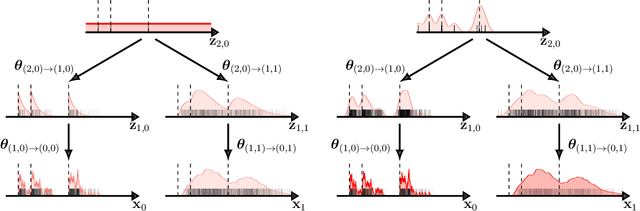
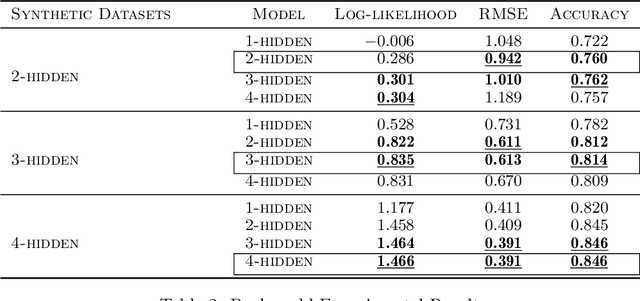
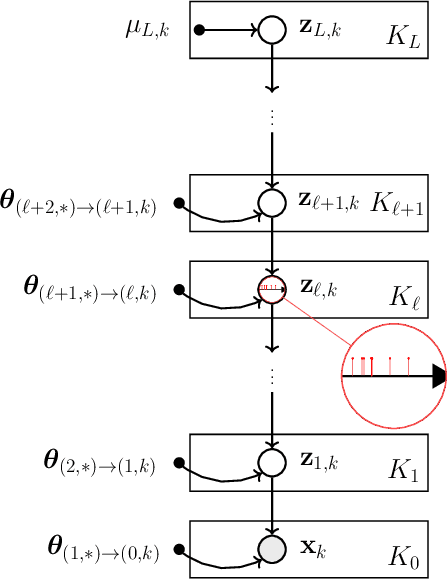
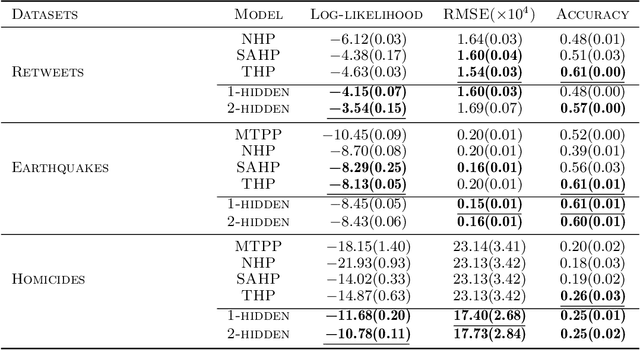
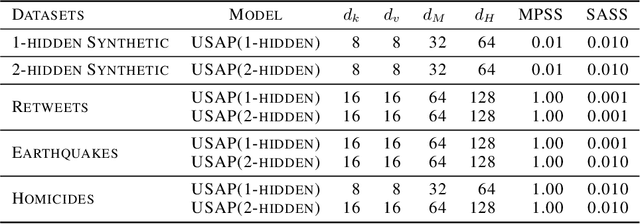
A Neyman-Scott process is a special case of a Cox process. The latent and observable stochastic processes are both Poisson processes. We consider a deep Neyman-Scott process in this paper, for which the building components of a network are all Poisson processes. We develop an efficient posterior sampling via Markov chain Monte Carlo and use it for likelihood-based inference. Our method opens up room for the inference in sophisticated hierarchical point processes. We show in the experiments that more hidden Poisson processes brings better performance for likelihood fitting and events types prediction. We also compare our method with state-of-the-art models for temporal real-world datasets and demonstrate competitive abilities for both data fitting and prediction, using far fewer parameters.

Convolutional Deep Exponential Families

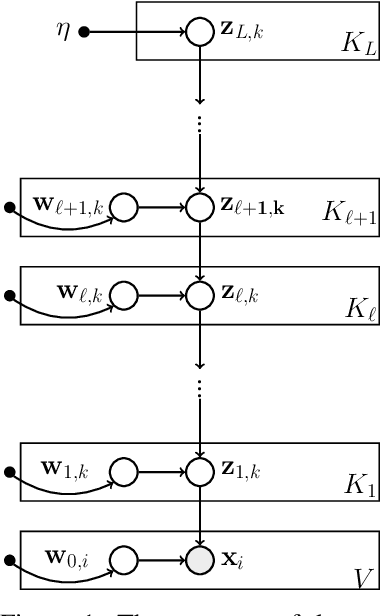
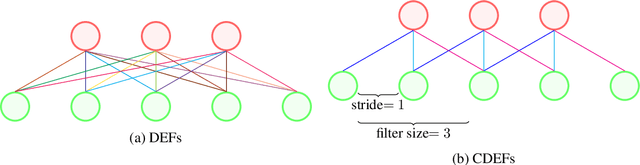
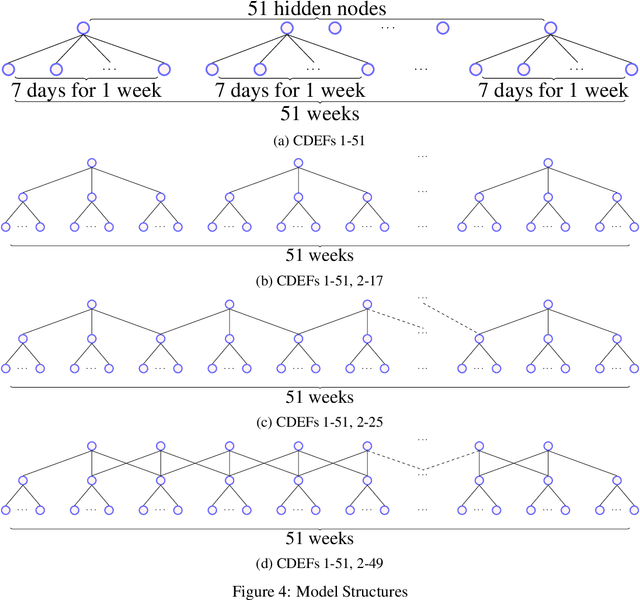
We describe convolutional deep exponential families (CDEFs) in this paper. CDEFs are built based on deep exponential families, deep probabilistic models that capture the hierarchical dependence between latent variables. CDEFs greatly reduce the number of free parameters by tying the weights of DEFs. Our experiments show that CDEFs are able to uncover time correlations with a small amount of data.

Intrusion Detection using Continuous Time Bayesian Networks

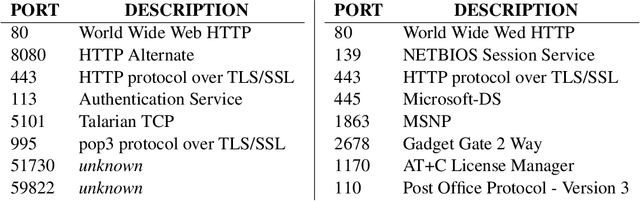
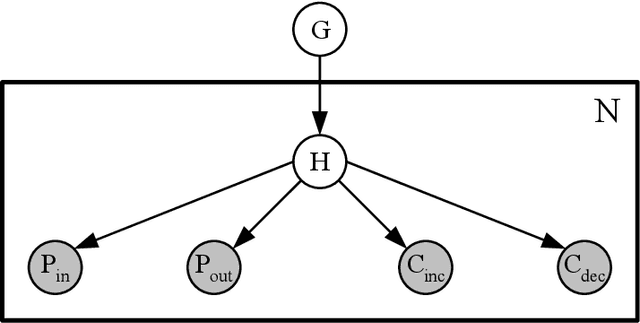
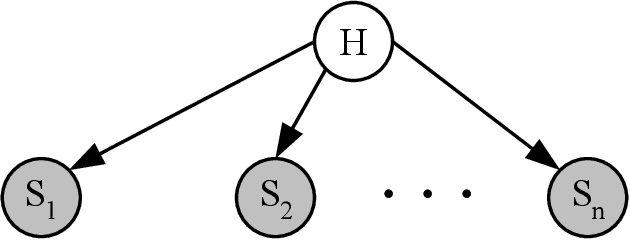
Intrusion detection systems (IDSs) fall into two high-level categories: network-based systems (NIDS) that monitor network behaviors, and host-based systems (HIDS) that monitor system calls. In this work, we present a general technique for both systems. We use anomaly detection, which identifies patterns not conforming to a historic norm. In both types of systems, the rates of change vary dramatically over time (due to burstiness) and over components (due to service difference). To efficiently model such systems, we use continuous time Bayesian networks (CTBNs) and avoid specifying a fixed update interval common to discrete-time models. We build generative models from the normal training data, and abnormal behaviors are flagged based on their likelihood under this norm. For NIDS, we construct a hierarchical CTBN model for the network packet traces and use Rao-Blackwellized particle filtering to learn the parameters. We illustrate the power of our method through experiments on detecting real worms and identifying hosts on two publicly available network traces, the MAWI dataset and the LBNL dataset. For HIDS, we develop a novel learning method to deal with the finite resolution of system log file time stamps, without losing the benefits of our continuous time model. We demonstrate the method by detecting intrusions in the DARPA 1998 BSM dataset.

Policy Improvement for POMDPs Using Normalized Importance Sampling

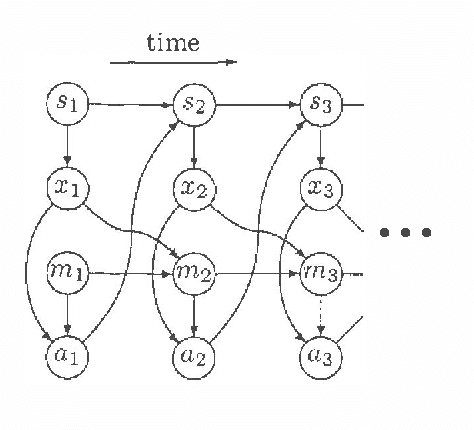
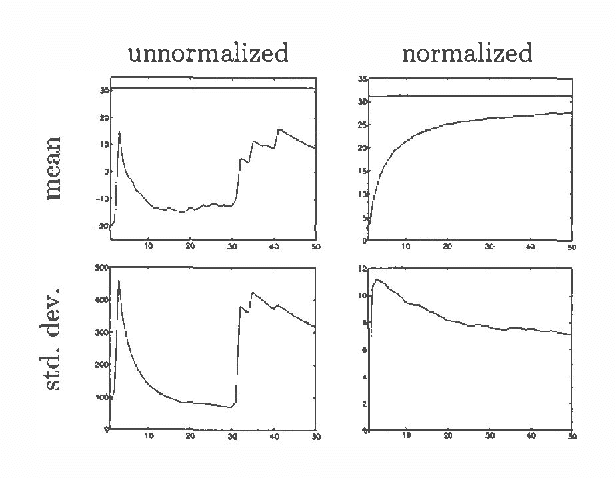
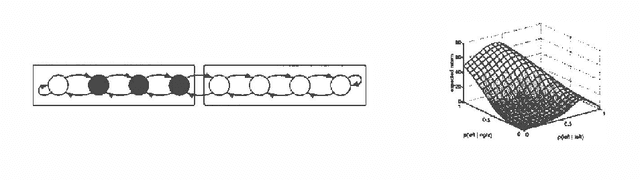
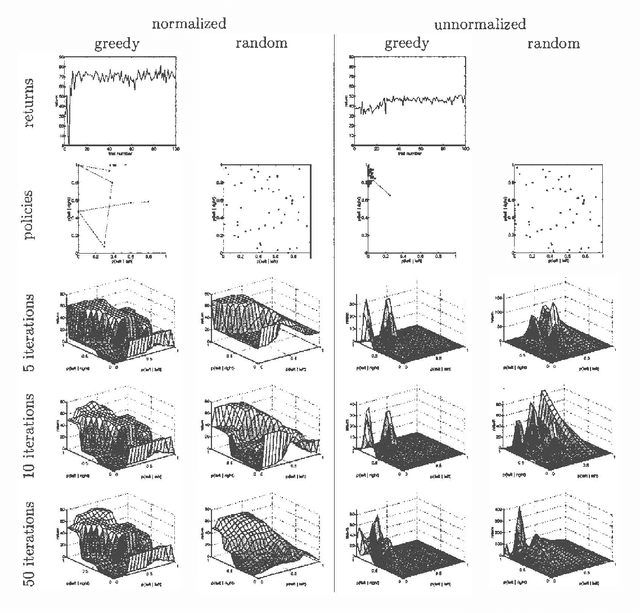
We present a new method for estimating the expected return of a POMDP from experience. The method does not assume any knowledge of the POMDP and allows the experience to be gathered from an arbitrary sequence of policies. The return is estimated for any new policy of the POMDP. We motivate the estimator from function-approximation and importance sampling points-of-view and derive its theoretical properties. Although the estimator is biased, it has low variance and the bias is often irrelevant when the estimator is used for pair-wise comparisons. We conclude by extending the estimator to policies with memory and compare its performance in a greedy search algorithm to REINFORCE algorithms showing an order of magnitude reduction in the number of trials required.

Reinforcement Learning with Partially Known World Dynamics

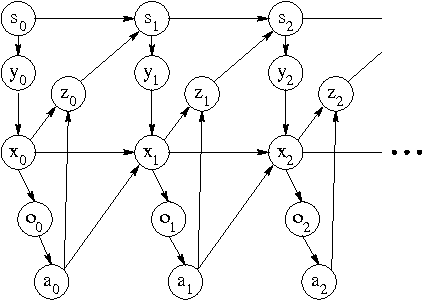
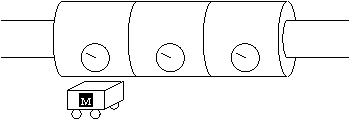
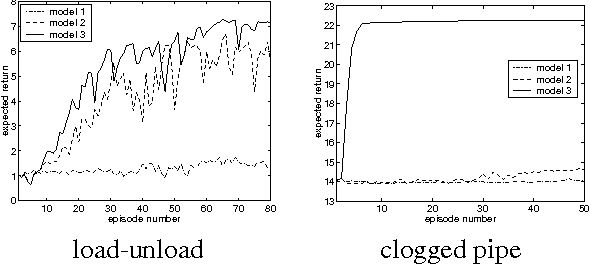
Reinforcement learning would enjoy better success on real-world problems if domain knowledge could be imparted to the algorithm by the modelers. Most problems have both hidden state and unknown dynamics. Partially observable Markov decision processes (POMDPs) allow for the modeling of both. Unfortunately, they do not provide a natural framework in which to specify knowledge about the domain dynamics. The designer must either admit to knowing nothing about the dynamics or completely specify the dynamics (thereby turning it into a planning problem). We propose a new framework called a partially known Markov decision process (PKMDP) which allows the designer to specify known dynamics while still leaving portions of the environment s dynamics unknown.The model represents NOT ONLY the environment dynamics but also the agents knowledge of the dynamics. We present a reinforcement learning algorithm for this model based on importance sampling. The algorithm incorporates planning based on the known dynamics and learning about the unknown dynamics. Our results clearly demonstrate the ability to add domain knowledge and the resulting benefits for learning.

Continuous Time Bayesian Networks

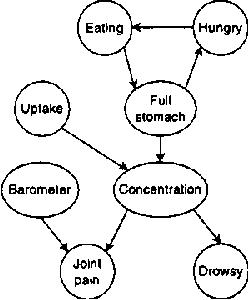
In this paper we present a language for finite state continuous time Bayesian networks (CTBNs), which describe structured stochastic processes that evolve over continuous time. The state of the system is decomposed into a set of local variables whose values change over time. The dynamics of the system are described by specifying the behavior of each local variable as a function of its parents in a directed (possibly cyclic) graph. The model specifies, at any given point in time, the distribution over two aspects: when a local variable changes its value and the next value it takes. These distributions are determined by the variable s CURRENT value AND the CURRENT VALUES OF its parents IN the graph.More formally, each variable IS modelled AS a finite state continuous time Markov process whose transition intensities are functions OF its parents.We present a probabilistic semantics FOR the language IN terms OF the generative model a CTBN defines OVER sequences OF events.We list types OF queries one might ask OF a CTBN, discuss the conceptual AND computational difficulties associated WITH exact inference, AND provide an algorithm FOR approximate inference which takes advantage OF the structure within the process.

Learning Continuous Time Bayesian Networks

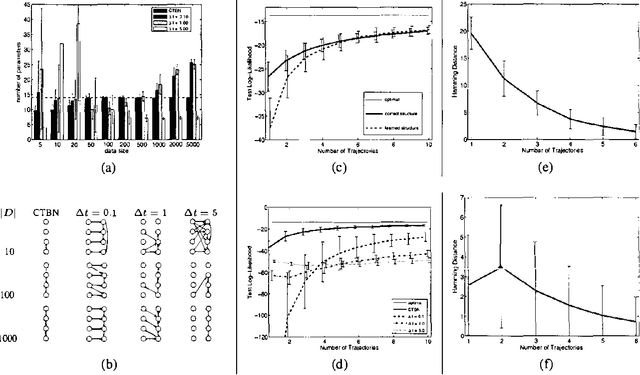
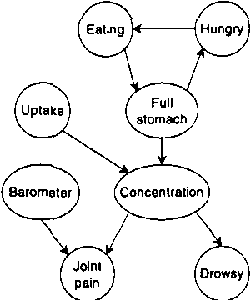
Continuous time Bayesian networks (CTBNs) describe structured stochastic processes with finitely many states that evolve over continuous time. A CTBN is a directed (possibly cyclic) dependency graph over a set of variables, each of which represents a finite state continuous time Markov process whose transition model is a function of its parents. We address the problem of learning parameters and structure of a CTBN from fully observed data. We define a conjugate prior for CTBNs, and show how it can be used both for Bayesian parameter estimation and as the basis of a Bayesian score for structure learning. Because acyclicity is not a constraint in CTBNs, we can show that the structure learning problem is significantly easier, both in theory and in practice, than structure learning for dynamic Bayesian networks (DBNs). Furthermore, as CTBNs can tailor the parameters and dependency structure to the different time granularities of the evolution of different variables, they can provide a better fit to continuous-time processes than DBNs with a fixed time granularity.

Expectation Maximization and Complex Duration Distributions for Continuous Time Bayesian Networks

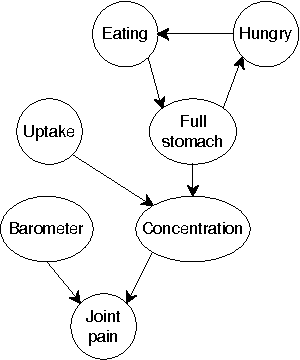
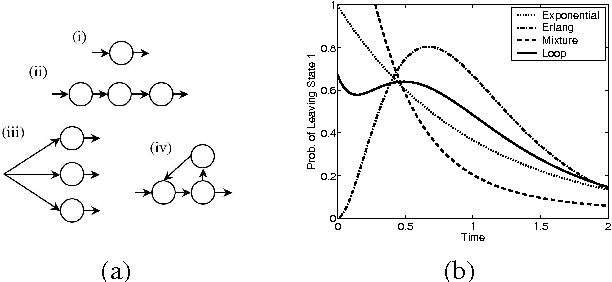
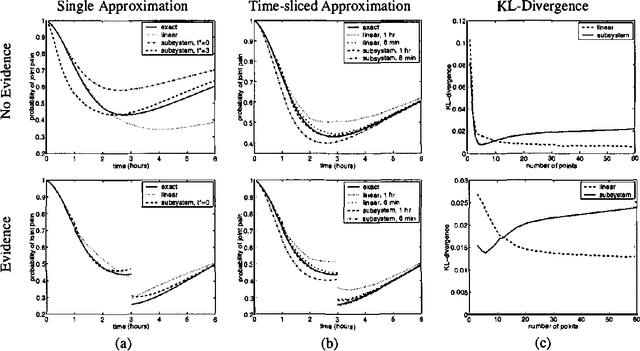
Continuous time Bayesian networks (CTBNs) describe structured stochastic processes with finitely many states that evolve over continuous time. A CTBN is a directed (possibly cyclic) dependency graph over a set of variables, each of which represents a finite state continuous time Markov process whose transition model is a function of its parents. We address the problem of learning the parameters and structure of a CTBN from partially observed data. We show how to apply expectation maximization (EM) and structural expectation maximization (SEM) to CTBNs. The availability of the EM algorithm allows us to extend the representation of CTBNs to allow a much richer class of transition durations distributions, known as phase distributions. This class is a highly expressive semi-parametric representation, which can approximate any duration distribution arbitrarily closely. This extension to the CTBN framework addresses one of the main limitations of both CTBNs and DBNs - the restriction to exponentially / geometrically distributed duration. We present experimental results on a real data set of people's life spans, showing that our algorithm learns reasonable models - structure and parameters - from partially observed data, and, with the use of phase distributions, achieves better performance than DBNs.

Expectation Propagation for Continuous Time Bayesian Networks

Continuous time Bayesian networks (CTBNs) describe structured stochastic processes with finitely many states that evolve over continuous time. A CTBN is a directed (possibly cyclic) dependency graph over a set of variables, each of which represents a finite state continuous time Markov process whose transition model is a function of its parents. As shown previously, exact inference in CTBNs is intractable. We address the problem of approximate inference, allowing for general queries conditioned on evidence over continuous time intervals and at discrete time points. We show how CTBNs can be parameterized within the exponential family, and use that insight to develop a message passing scheme in cluster graphs and allows us to apply expectation propagation to CTBNs. The clusters in our cluster graph do not contain distributions over the cluster variables at individual time points, but distributions over trajectories of the variables throughout a duration. Thus, unlike discrete time temporal models such as dynamic Bayesian networks, we can adapt the time granularity at which we reason for different variables and in different conditions.