Variational Inference for Neyman-Scott Processes

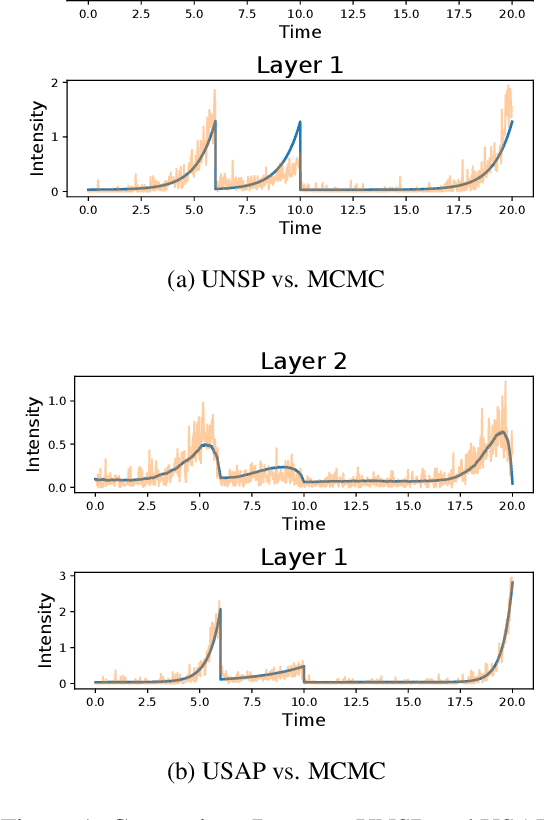
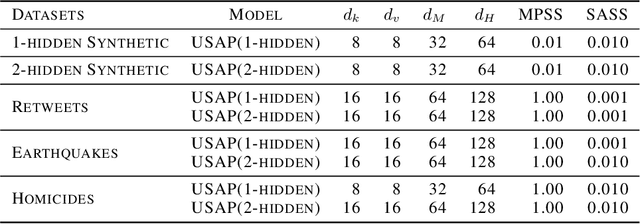
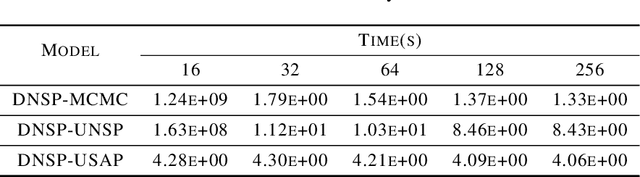
Neyman-Scott processes (NSPs) have been applied across a range of fields to model points or temporal events with a hierarchy of clusters. Markov chain Monte Carlo (MCMC) is typically used for posterior sampling in the model. However, MCMC's mixing time can cause the resulting inference to be slow, and thereby slow down model learning and prediction. We develop the first variational inference (VI) algorithm for NSPs, and give two examples of suitable variational posterior point process distributions. Our method minimizes the inclusive Kullback-Leibler (KL) divergence for VI to obtain the variational parameters. We generate samples from the approximate posterior point processes much faster than MCMC, as we can directly estimate the approximate posterior point processes without any MCMC steps or gradient descent. We include synthetic and real-world data experiments that demonstrate our VI algorithm achieves better prediction performance than MCMC when computational time is limited.

Deep Neyman-Scott Processes

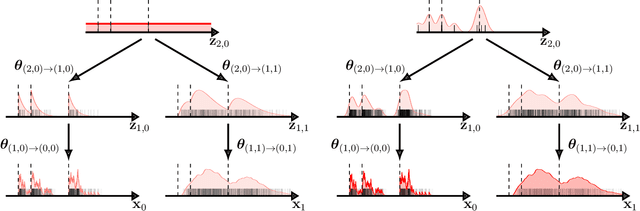
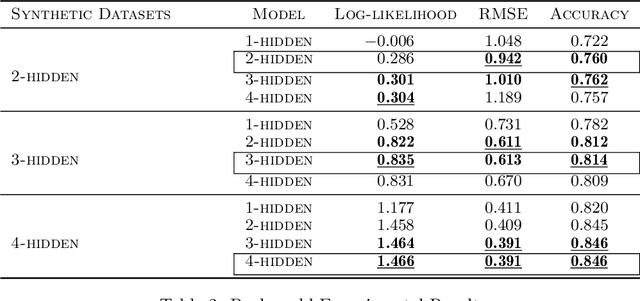
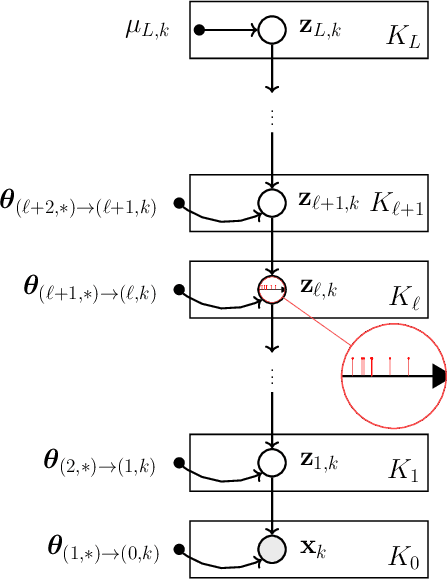
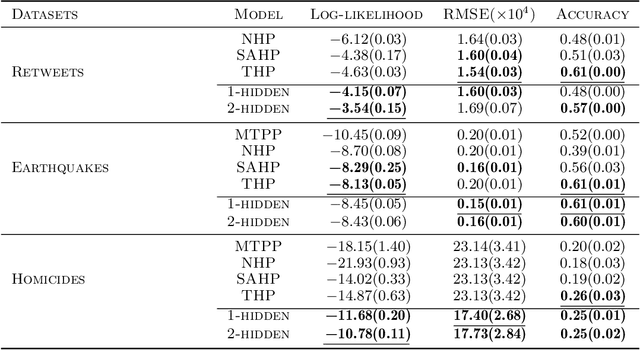
A Neyman-Scott process is a special case of a Cox process. The latent and observable stochastic processes are both Poisson processes. We consider a deep Neyman-Scott process in this paper, for which the building components of a network are all Poisson processes. We develop an efficient posterior sampling via Markov chain Monte Carlo and use it for likelihood-based inference. Our method opens up room for the inference in sophisticated hierarchical point processes. We show in the experiments that more hidden Poisson processes brings better performance for likelihood fitting and events types prediction. We also compare our method with state-of-the-art models for temporal real-world datasets and demonstrate competitive abilities for both data fitting and prediction, using far fewer parameters.

Convolutional Deep Exponential Families

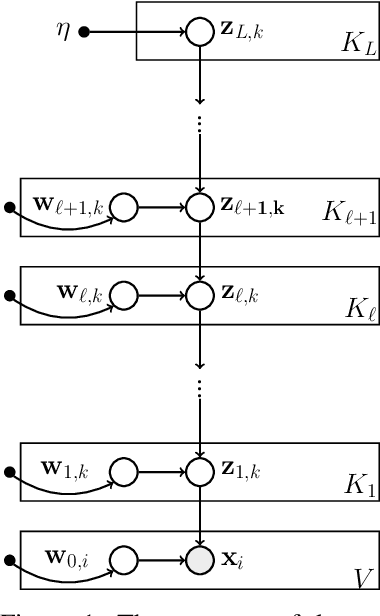
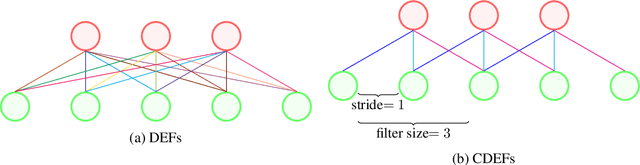
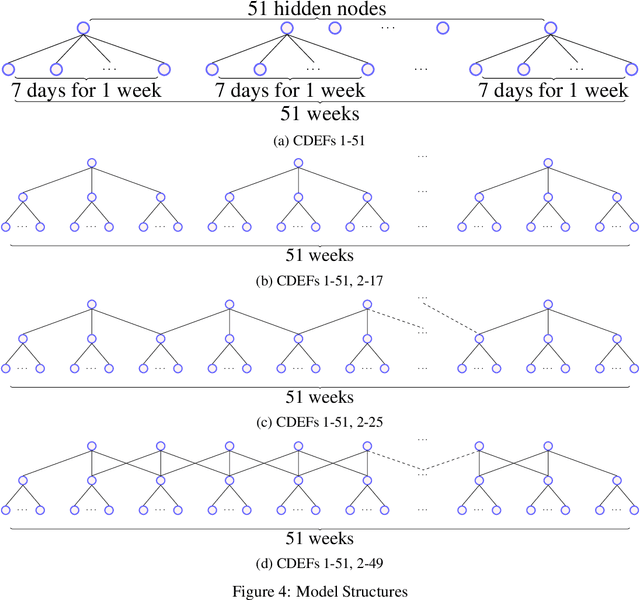
We describe convolutional deep exponential families (CDEFs) in this paper. CDEFs are built based on deep exponential families, deep probabilistic models that capture the hierarchical dependence between latent variables. CDEFs greatly reduce the number of free parameters by tying the weights of DEFs. Our experiments show that CDEFs are able to uncover time correlations with a small amount of data.