Continuous Time Bayesian Networks
Paper and Code
Dec 12, 2012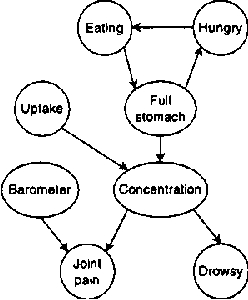
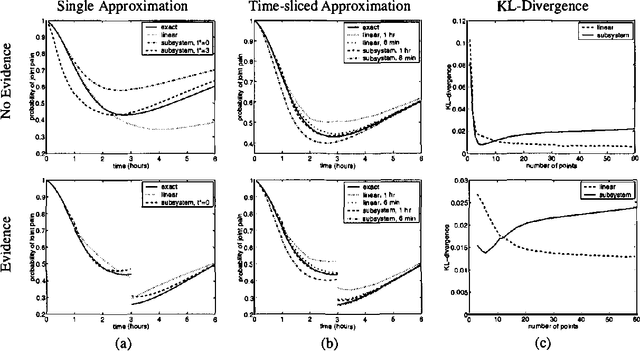
In this paper we present a language for finite state continuous time Bayesian networks (CTBNs), which describe structured stochastic processes that evolve over continuous time. The state of the system is decomposed into a set of local variables whose values change over time. The dynamics of the system are described by specifying the behavior of each local variable as a function of its parents in a directed (possibly cyclic) graph. The model specifies, at any given point in time, the distribution over two aspects: when a local variable changes its value and the next value it takes. These distributions are determined by the variable s CURRENT value AND the CURRENT VALUES OF its parents IN the graph.More formally, each variable IS modelled AS a finite state continuous time Markov process whose transition intensities are functions OF its parents.We present a probabilistic semantics FOR the language IN terms OF the generative model a CTBN defines OVER sequences OF events.We list types OF queries one might ask OF a CTBN, discuss the conceptual AND computational difficulties associated WITH exact inference, AND provide an algorithm FOR approximate inference which takes advantage OF the structure within the process.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge