Continuous Time Bayesian Networks

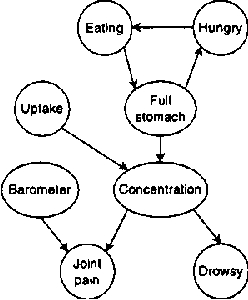
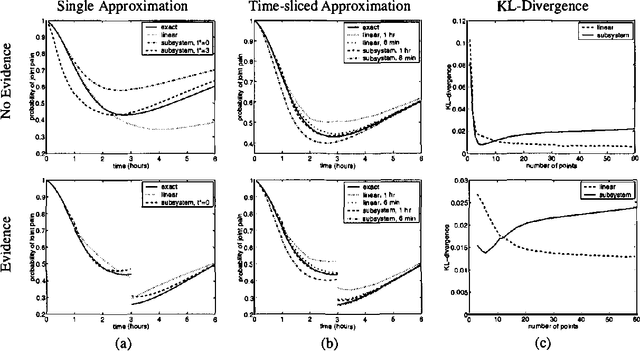
In this paper we present a language for finite state continuous time Bayesian networks (CTBNs), which describe structured stochastic processes that evolve over continuous time. The state of the system is decomposed into a set of local variables whose values change over time. The dynamics of the system are described by specifying the behavior of each local variable as a function of its parents in a directed (possibly cyclic) graph. The model specifies, at any given point in time, the distribution over two aspects: when a local variable changes its value and the next value it takes. These distributions are determined by the variable s CURRENT value AND the CURRENT VALUES OF its parents IN the graph.More formally, each variable IS modelled AS a finite state continuous time Markov process whose transition intensities are functions OF its parents.We present a probabilistic semantics FOR the language IN terms OF the generative model a CTBN defines OVER sequences OF events.We list types OF queries one might ask OF a CTBN, discuss the conceptual AND computational difficulties associated WITH exact inference, AND provide an algorithm FOR approximate inference which takes advantage OF the structure within the process.

Learning Continuous Time Bayesian Networks

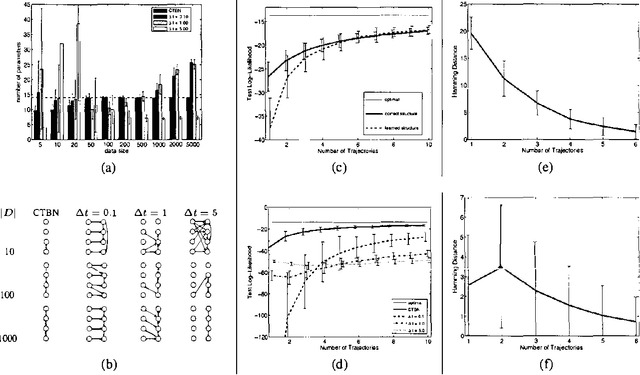
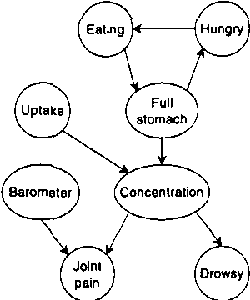
Continuous time Bayesian networks (CTBNs) describe structured stochastic processes with finitely many states that evolve over continuous time. A CTBN is a directed (possibly cyclic) dependency graph over a set of variables, each of which represents a finite state continuous time Markov process whose transition model is a function of its parents. We address the problem of learning parameters and structure of a CTBN from fully observed data. We define a conjugate prior for CTBNs, and show how it can be used both for Bayesian parameter estimation and as the basis of a Bayesian score for structure learning. Because acyclicity is not a constraint in CTBNs, we can show that the structure learning problem is significantly easier, both in theory and in practice, than structure learning for dynamic Bayesian networks (DBNs). Furthermore, as CTBNs can tailor the parameters and dependency structure to the different time granularities of the evolution of different variables, they can provide a better fit to continuous-time processes than DBNs with a fixed time granularity.

Expectation Maximization and Complex Duration Distributions for Continuous Time Bayesian Networks

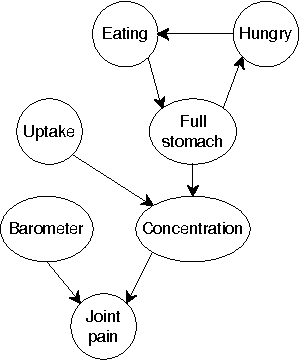
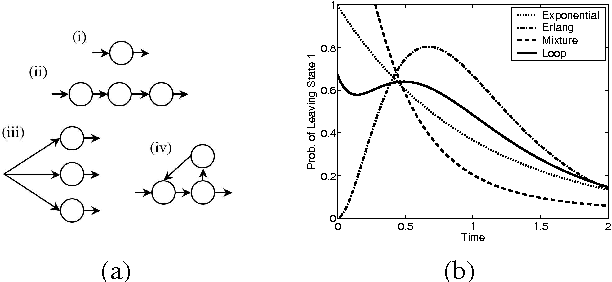
Continuous time Bayesian networks (CTBNs) describe structured stochastic processes with finitely many states that evolve over continuous time. A CTBN is a directed (possibly cyclic) dependency graph over a set of variables, each of which represents a finite state continuous time Markov process whose transition model is a function of its parents. We address the problem of learning the parameters and structure of a CTBN from partially observed data. We show how to apply expectation maximization (EM) and structural expectation maximization (SEM) to CTBNs. The availability of the EM algorithm allows us to extend the representation of CTBNs to allow a much richer class of transition durations distributions, known as phase distributions. This class is a highly expressive semi-parametric representation, which can approximate any duration distribution arbitrarily closely. This extension to the CTBN framework addresses one of the main limitations of both CTBNs and DBNs - the restriction to exponentially / geometrically distributed duration. We present experimental results on a real data set of people's life spans, showing that our algorithm learns reasonable models - structure and parameters - from partially observed data, and, with the use of phase distributions, achieves better performance than DBNs.

Expectation Propagation for Continuous Time Bayesian Networks

Continuous time Bayesian networks (CTBNs) describe structured stochastic processes with finitely many states that evolve over continuous time. A CTBN is a directed (possibly cyclic) dependency graph over a set of variables, each of which represents a finite state continuous time Markov process whose transition model is a function of its parents. As shown previously, exact inference in CTBNs is intractable. We address the problem of approximate inference, allowing for general queries conditioned on evidence over continuous time intervals and at discrete time points. We show how CTBNs can be parameterized within the exponential family, and use that insight to develop a message passing scheme in cluster graphs and allows us to apply expectation propagation to CTBNs. The clusters in our cluster graph do not contain distributions over the cluster variables at individual time points, but distributions over trajectories of the variables throughout a duration. Thus, unlike discrete time temporal models such as dynamic Bayesian networks, we can adapt the time granularity at which we reason for different variables and in different conditions.

Reasoning at the Right Time Granularity

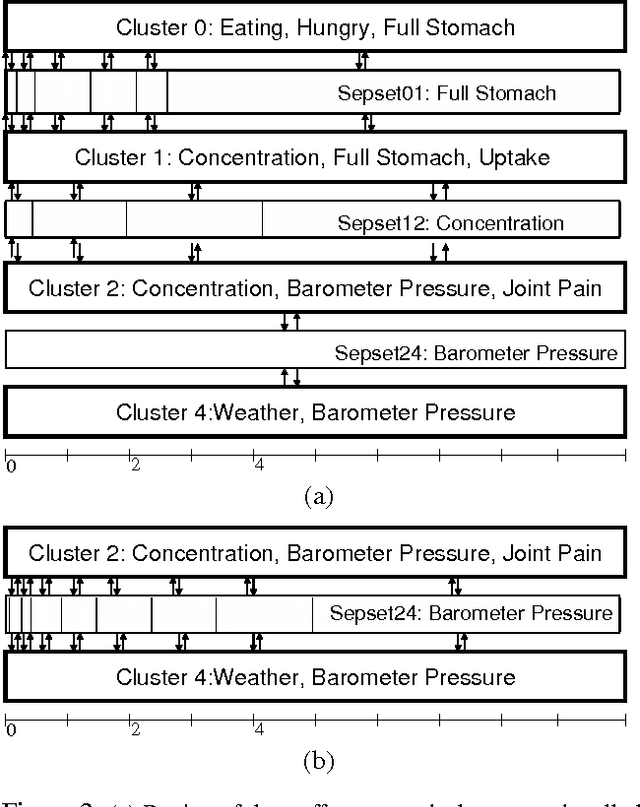
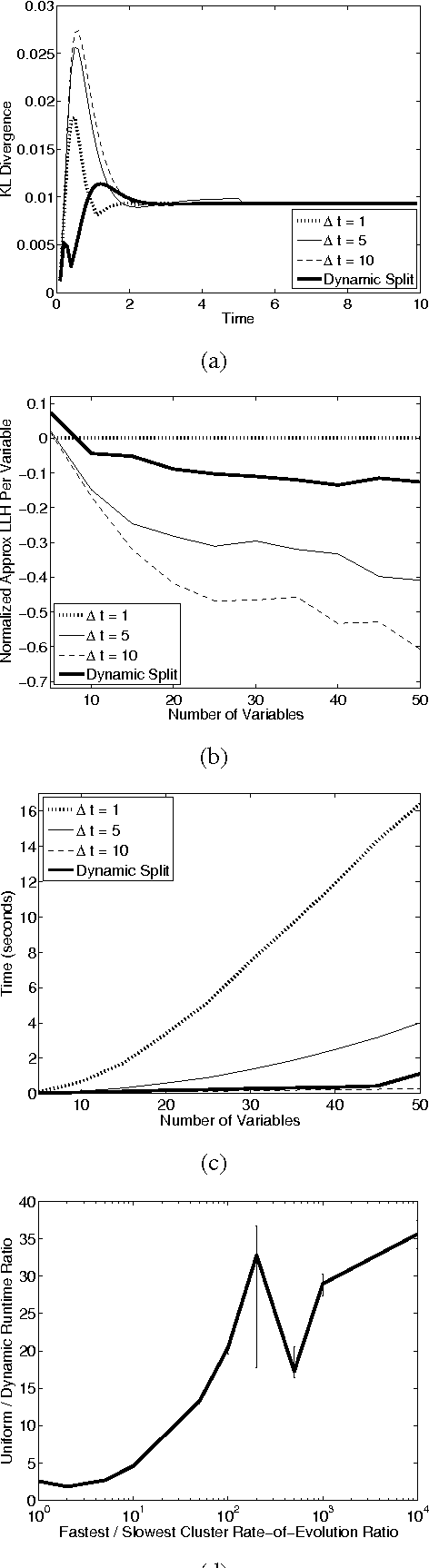
Most real-world dynamic systems are composed of different components that often evolve at very different rates. In traditional temporal graphical models, such as dynamic Bayesian networks, time is modeled at a fixed granularity, generally selected based on the rate at which the fastest component evolves. Inference must then be performed at this fastest granularity, potentially at significant computational cost. Continuous Time Bayesian Networks (CTBNs) avoid time-slicing in the representation by modeling the system as evolving continuously over time. The expectation-propagation (EP) inference algorithm of Nodelman et al. (2005) can then vary the inference granularity over time, but the granularity is uniform across all parts of the system, and must be selected in advance. In this paper, we provide a new EP algorithm that utilizes a general cluster graph architecture where clusters contain distributions that can overlap in both space (set of variables) and time. This architecture allows different parts of the system to be modeled at very different time granularities, according to their current rate of evolution. We also provide an information-theoretic criterion for dynamically re-partitioning the clusters during inference to tune the level of approximation to the current rate of evolution. This avoids the need to hand-select the appropriate granularity, and allows the granularity to adapt as information is transmitted across the network. We present experiments demonstrating that this approach can result in significant computational savings.