Reasoning at the Right Time Granularity
Paper and Code
Jun 20, 2012
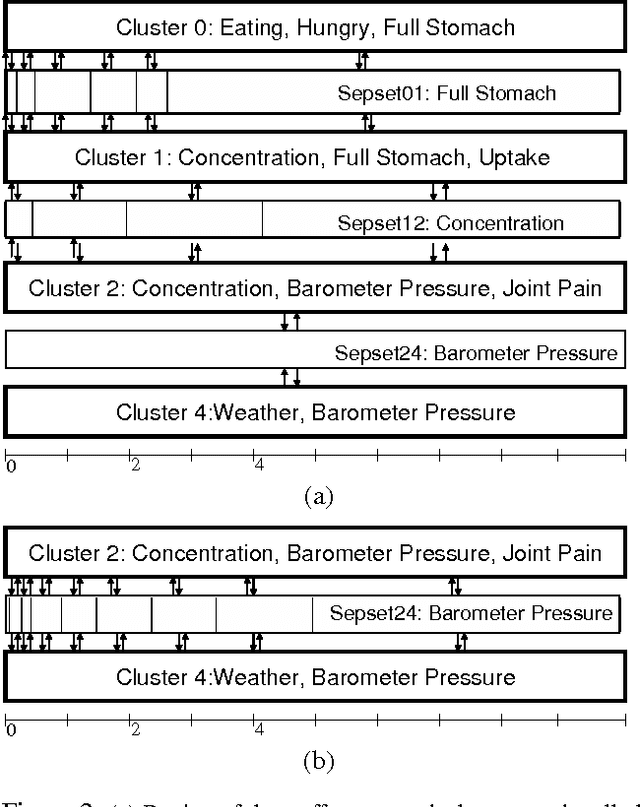
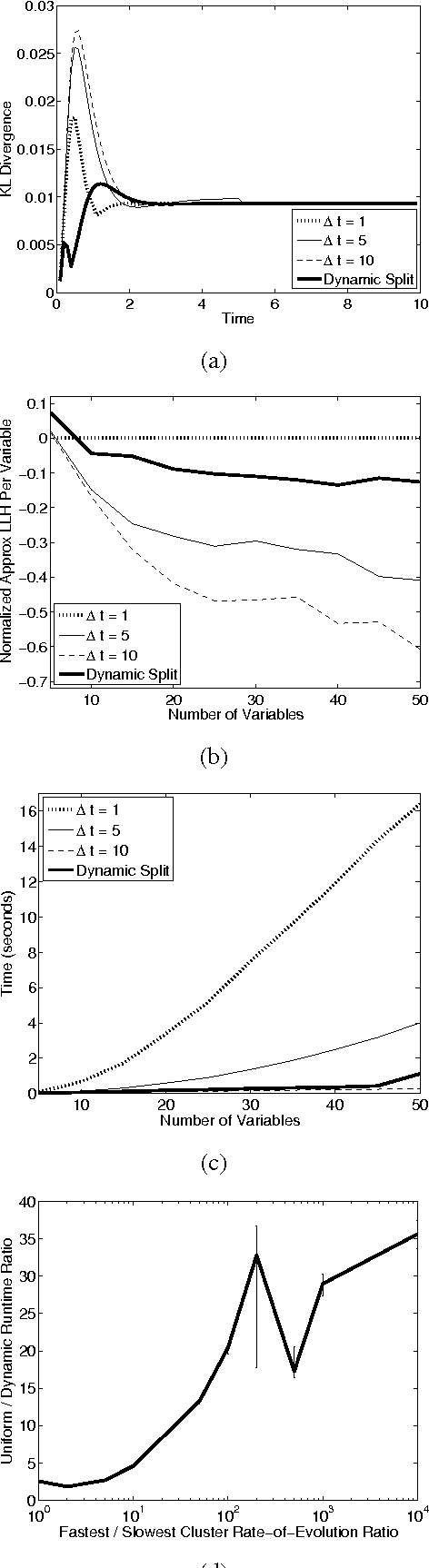
Most real-world dynamic systems are composed of different components that often evolve at very different rates. In traditional temporal graphical models, such as dynamic Bayesian networks, time is modeled at a fixed granularity, generally selected based on the rate at which the fastest component evolves. Inference must then be performed at this fastest granularity, potentially at significant computational cost. Continuous Time Bayesian Networks (CTBNs) avoid time-slicing in the representation by modeling the system as evolving continuously over time. The expectation-propagation (EP) inference algorithm of Nodelman et al. (2005) can then vary the inference granularity over time, but the granularity is uniform across all parts of the system, and must be selected in advance. In this paper, we provide a new EP algorithm that utilizes a general cluster graph architecture where clusters contain distributions that can overlap in both space (set of variables) and time. This architecture allows different parts of the system to be modeled at very different time granularities, according to their current rate of evolution. We also provide an information-theoretic criterion for dynamically re-partitioning the clusters during inference to tune the level of approximation to the current rate of evolution. This avoids the need to hand-select the appropriate granularity, and allows the granularity to adapt as information is transmitted across the network. We present experiments demonstrating that this approach can result in significant computational savings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge