A matrix-free Levenberg-Marquardt algorithm for efficient ptychographic phase retrieval

The phase retrieval problem, where one aims to recover a complex-valued image from far-field intensity measurements, is a classic problem encountered in a range of imaging applications. Modern phase retrieval approaches usually rely on gradient descent methods in a nonlinear minimization framework. Calculating closed-form gradients for use in these methods is tedious work, and formulating second order derivatives is even more laborious. Additionally, second order techniques often require the storage and inversion of large matrices of partial derivatives, with memory requirements that can be prohibitive for data-rich imaging modalities. We use a reverse-mode automatic differentiation (AD) framework to implement an efficient matrix-free version of the Levenberg-Marquardt (LM) algorithm, a longstanding method that finds popular use in nonlinear least-square minimization problems but which has seen little use in phase retrieval. Furthermore, we extend the basic LM algorithm so that it can be applied for general constrained optimization problems beyond just the least-square applications. Since we use AD, we only need to specify the physics-based forward model for a specific imaging application; the derivative terms are calculated automatically through matrix-vector products, without explicitly forming any large Jacobian or Gauss-Newton matrices. We demonstrate that this algorithm can be used to solve both the unconstrained ptychographic object retrieval problem and the constrained "blind" ptychographic object and probe retrieval problems, under both the Gaussian and Poisson noise models, and that this method outperforms best-in-class first-order ptychographic reconstruction methods: it provides excellent convergence guarantees with (in many cases) a superlinear rate of convergence, all with a computational cost comparable to, or lower than, the tested first-order algorithms.

Using a modified double deep image prior for crosstalk mitigation in multislice ptychography

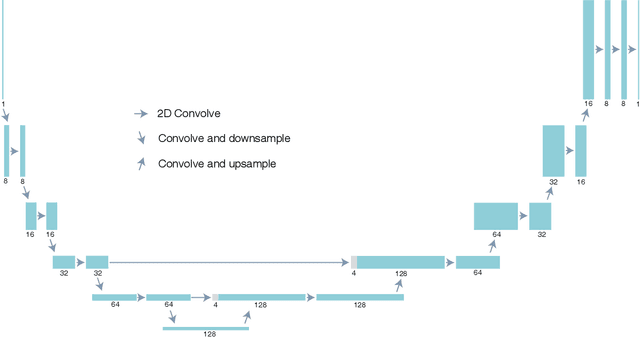
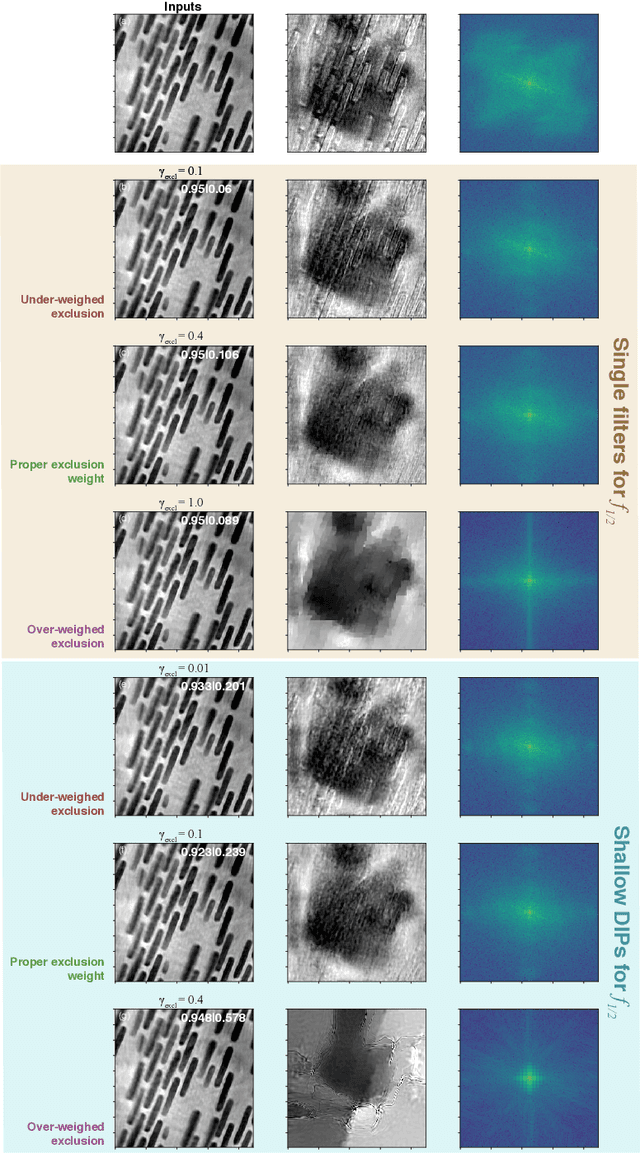
Multislice ptychography is a high-resolution microscopy technique used to image multiple separate axial planes using a single illumination direction. However, multislice ptychography reconstructions are often degraded by crosstalk, where some features on one plane erroneously contribute to the reconstructed image of another plane. Here, we demonstrate the use of a modified "double deep image prior" (DDIP) architecture in mitigating crosstalk artifacts in multislice ptychography. Utilizing the tendency of generative neural networks to produce natural images, a modified DDIP method yielded good results on experimental data. For one of the datasets, we show that using DDIP could remove the need of using additional experimental data, such as from x-ray fluorescence, to suppress the crosstalk. Our method may help x-ray multislice ptychography work for more general experimental scenarios.

Adorym: A multi-platform generic x-ray image reconstruction framework based on automatic differentiation

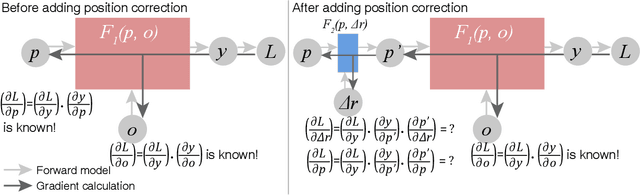
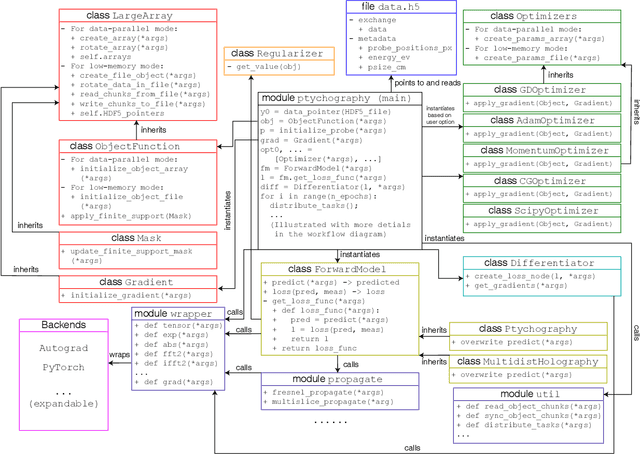
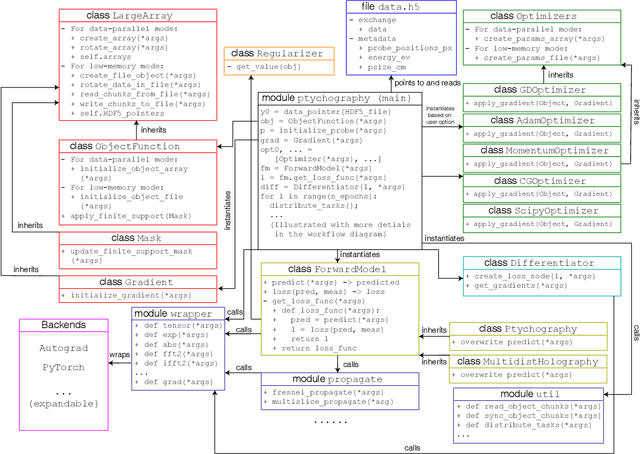
We describe and demonstrate an optimization-based x-ray image reconstruction framework called Adorym. Our framework provides a generic forward model, allowing one code framework to be used for a wide range of imaging methods ranging from near-field holography to and fly-scan ptychographic tomography. By using automatic differentiation for optimization, Adorym has the flexibility to refine experimental parameters including probe positions, multiple hologram alignment, and object tilts. It is written with strong support for parallel processing, allowing large datasets to be processed on high-performance computing systems. We demonstrate its use on several experimental datasets to show improved image quality through parameter refinement.

Quantifying mesoscale neuroanatomy using X-ray microtomography

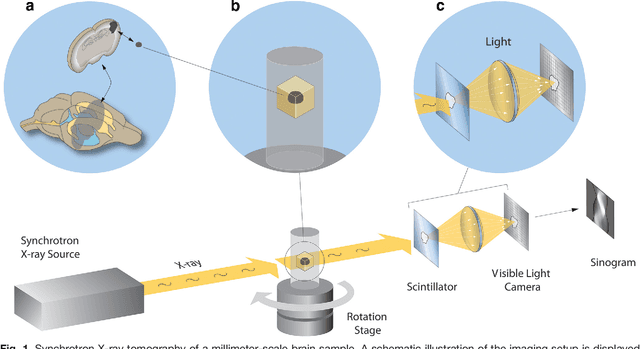
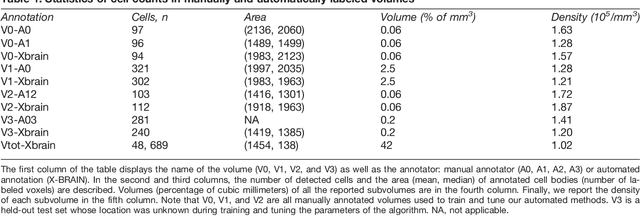
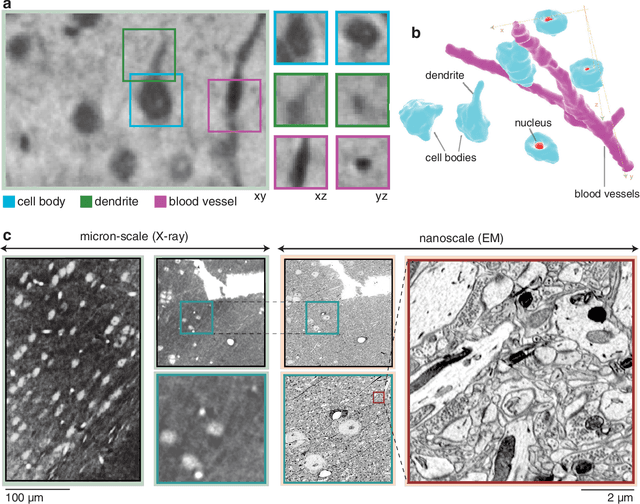
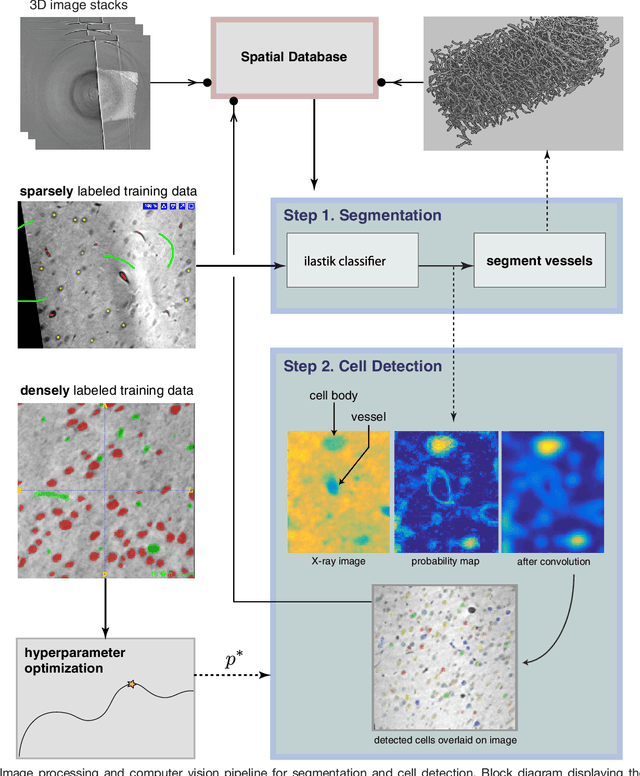
Methods for resolving the 3D microstructure of the brain typically start by thinly slicing and staining the brain, and then imaging each individual section with visible light photons or electrons. In contrast, X-rays can be used to image thick samples, providing a rapid approach for producing large 3D brain maps without sectioning. Here we demonstrate the use of synchrotron X-ray microtomography ($\mu$CT) for producing mesoscale $(1~\mu m^3)$ resolution brain maps from millimeter-scale volumes of mouse brain. We introduce a pipeline for $\mu$CT-based brain mapping that combines methods for sample preparation, imaging, automated segmentation of image volumes into cells and blood vessels, and statistical analysis of the resulting brain structures. Our results demonstrate that X-ray tomography promises rapid quantification of large brain volumes, complementing other brain mapping and connectomics efforts.