A differentiable forward model for the concurrent, multi-peak Bragg coherent x-ray diffraction imaging problem

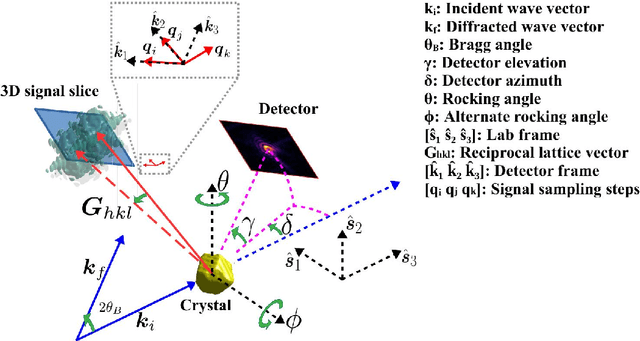
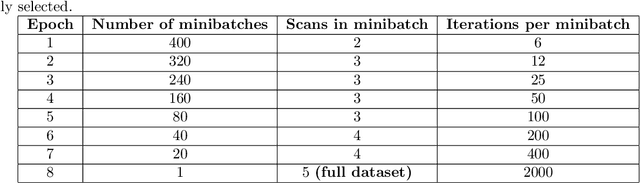
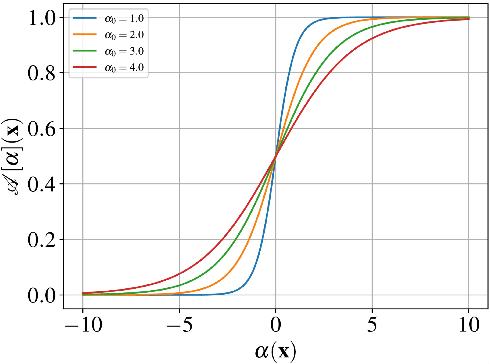
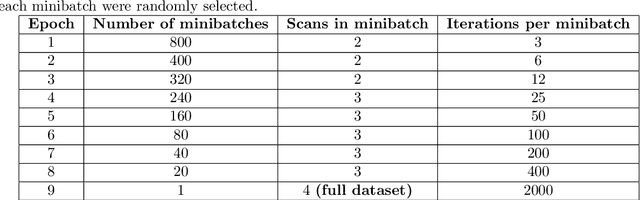
We present a general analytic approach to spatially resolve the nano-scale lattice distortion field of strained and defected compact crystals with Bragg coherent x-ray diffraction imaging (BCDI). Our approach relies on fitting a differentiable forward model simultaneously to multiple BCDI datasets corresponding to independent Bragg reflections from the same single crystal. It is designed to be faithful to heterogeneities that potentially manifest as phase discontinuities in the coherently diffracted wave, such as lattice dislocations in an imperfect crystal. We retain fidelity to such small features in the reconstruction process through a Fourier transform -based resampling algorithm designed to largely avoid the point spread tendencies of commonly employed interpolation methods. The reconstruction model defined in this manner brings BCDI reconstruction into the scope of explicit optimization driven by automatic differentiation. With results from simulations and experimental diffraction data, we demonstrate significant improvement in the final image quality compared to conventional phase retrieval, enabled by explicitly coupling multiple BCDI datasets into the reconstruction loss function.

A matrix-free Levenberg-Marquardt algorithm for efficient ptychographic phase retrieval

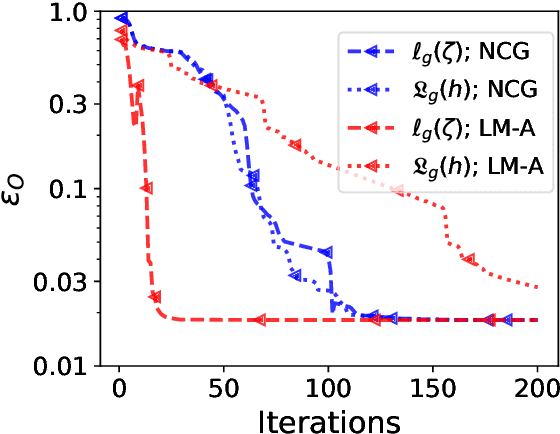
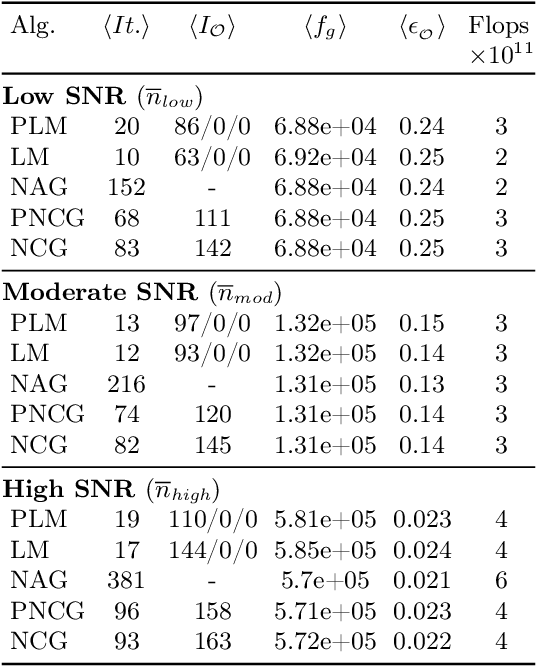
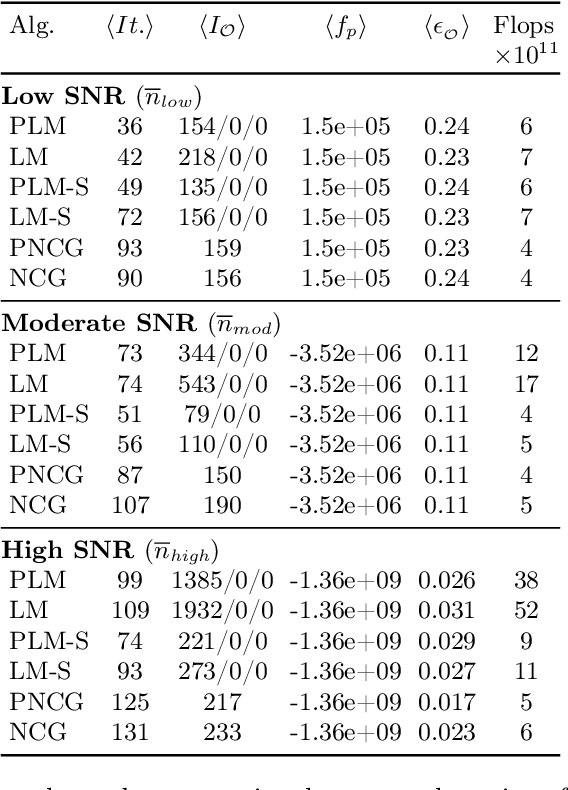
The phase retrieval problem, where one aims to recover a complex-valued image from far-field intensity measurements, is a classic problem encountered in a range of imaging applications. Modern phase retrieval approaches usually rely on gradient descent methods in a nonlinear minimization framework. Calculating closed-form gradients for use in these methods is tedious work, and formulating second order derivatives is even more laborious. Additionally, second order techniques often require the storage and inversion of large matrices of partial derivatives, with memory requirements that can be prohibitive for data-rich imaging modalities. We use a reverse-mode automatic differentiation (AD) framework to implement an efficient matrix-free version of the Levenberg-Marquardt (LM) algorithm, a longstanding method that finds popular use in nonlinear least-square minimization problems but which has seen little use in phase retrieval. Furthermore, we extend the basic LM algorithm so that it can be applied for general constrained optimization problems beyond just the least-square applications. Since we use AD, we only need to specify the physics-based forward model for a specific imaging application; the derivative terms are calculated automatically through matrix-vector products, without explicitly forming any large Jacobian or Gauss-Newton matrices. We demonstrate that this algorithm can be used to solve both the unconstrained ptychographic object retrieval problem and the constrained "blind" ptychographic object and probe retrieval problems, under both the Gaussian and Poisson noise models, and that this method outperforms best-in-class first-order ptychographic reconstruction methods: it provides excellent convergence guarantees with (in many cases) a superlinear rate of convergence, all with a computational cost comparable to, or lower than, the tested first-order algorithms.