Monte Carlo Forest Search: UNSAT Solver Synthesis via Reinforcement learning

We introduce Monte Carlo Forest Search (MCFS), an offline algorithm for automatically synthesizing strong tree-search solvers for proving \emph{unsatisfiability} on given distributions, leveraging ideas from the Monte Carlo Tree Search (MCTS) algorithm that led to breakthroughs in AlphaGo. The crucial difference between proving unsatisfiability and existing applications of MCTS, is that policies produce trees rather than paths. Rather than finding a good path (solution) within a tree, the search problem becomes searching for a small proof tree within a forest of candidate proof trees. We introduce two key ideas to adapt to this setting. First, we estimate tree size with paths, via the unbiased approximation from Knuth (1975). Second, we query a strong solver at a user-defined depth rather than learning a policy across the whole tree, in order to focus our policy search on early decisions, which offer the greatest potential for reducing tree size. We then present MCFS-SAT, an implementation of MCFS for learning branching policies for solving the Boolean satisfiability (SAT) problem that required many modifications from AlphaGo. We matched or improved performance over a strong baseline on two well-known SAT distributions (\texttt{sgen}, \texttt{random}). Notably, we improved running time by 9\% on \texttt{sgen} over the \texttt{kcnfs} solver and even further over the strongest UNSAT solver from the 2021 SAT competition.

Matching Papers and Reviewers at Large Conferences

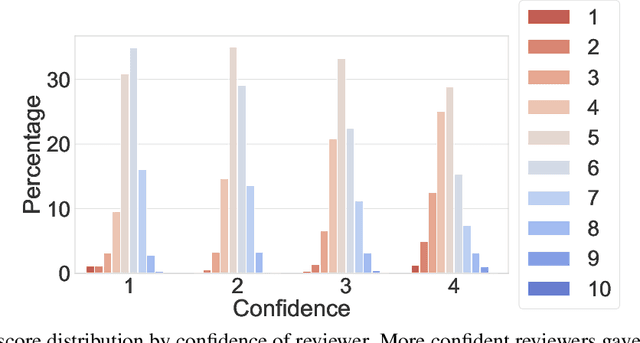
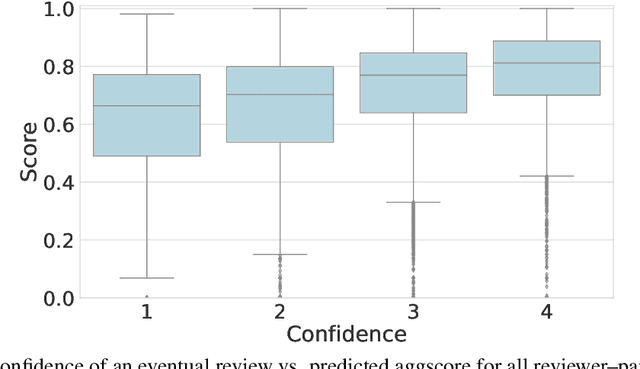
This paper studies a novel reviewer-paper matching approach that was recently deployed in the 35th AAAI Conference on Artificial Intelligence (AAAI 2021), and has since been adopted by other conferences including AAAI 2022 and ICML 2022. This approach has three main elements: (1) collecting and processing input data to identify problematic matches and generate reviewer-paper scores; (2) formulating and solving an optimization problem to find good reviewer-paper matchings; and (3) the introduction of a novel, two-phase reviewing process that shifted reviewing resources away from papers likely to be rejected and towards papers closer to the decision boundary. This paper also describes an evaluation of these innovations based on an extensive post-hoc analysis on real data -- including a comparison with the matching algorithm used in AAAI's previous (2020) iteration -- and supplements this with additional numerical experimentation.

The Perils of Learning Before Optimizing

Formulating real-world optimization problems often begins with making predictions from historical data (e.g., an optimizer that aims to recommend fast routes relies upon travel-time predictions). Typically, learning the prediction model used to generate the optimization problem and solving that problem are performed in two separate stages. Recent work has showed how such prediction models can be learned end-to-end by differentiating through the optimization task. Such methods often yield empirical improvements, which are typically attributed to end-to-end making better error tradeoffs than the standard loss function used in a two-stage solution. We refine this explanation and more precisely characterize when end-to-end can improve performance. When prediction targets are stochastic, a two-stage solution must make an a priori choice about which statistics of the target distribution to model -- we consider expectations over prediction targets -- while an end-to-end solution can make this choice adaptively. We show that the performance gap between a two-stage and end-to-end approach is closely related to the \emph{price of correlation} concept in stochastic optimization and show the implications of some existing POC results for our predict-then-optimize problem. We then consider a novel and particularly practical setting, where coefficients in the objective function depend on multiple prediction targets. We give explicit constructions where (1) two-stage performs unboundedly worse than end-to-end; and (2) two-stage is optimal. We identify a large set of real-world applications whose objective functions rely on multiple prediction targets but which nevertheless deploy two-stage solutions. We also use simulations to experimentally quantify performance gaps.