Continuous Angular Power Spectrum Recovery From Channel Covariance via Chebyshev Polynomials

This paper proposes a Chebyshev polynomial expansion framework for the recovery of a continuous angular power spectrum (APS) from channel covariance. By exploiting the orthogonality of Chebyshev polynomials in a transformed domain, we derive an exact series representation of the covariance and reformulate the inherently ill-posed APS inversion as a finite-dimensional linear regression problem via truncation. The associated approximation error is directly controlled by the tail of the APS's Chebyshev series and decays rapidly with increasing angular smoothness. Building on this representation, we derive an exact semidefinite characterization of nonnegative APS and introduce a derivative-based regularizer that promotes smoothly varying APS profiles while preserving transitions of clusters. Simulation results show that the proposed Chebyshev-based framework yields accurate APS reconstruction, and enables reliable downlink (DL) covariance prediction from uplink (UL) measurements in a frequency division duplex (FDD) setting. These findings indicate that jointly exploiting smoothness and nonnegativity in a Chebyshev domain provides an effective tool for covariance-domain processing in multi-antenna systems.

Affine-Projection Recovery of Continuous Angular Power Spectrum: Geometry and Resolution

This paper considers recovering a continuous angular power spectrum (APS) from the channel covariance. Building on the projection-onto-linear-variety (PLV) algorithm, an affine-projection approach introduced by Miretti \emph{et. al.}, we analyze PLV in a well-defined \emph{weighted} Fourier-domain to emphasize its geometric interpretability. This yields an explicit fixed-dimensional trigonometric-polynomial representation and a closed-form solution via a positive-definite matrix, which directly implies uniqueness. We further establish an exact energy identity that yields the APS reconstruction error and leads to a sharp identifiability/resolution characterization: PLV achieves perfect recovery if and only if the ground-truth APS lies in the identified trigonometric-polynomial subspace; otherwise it returns the minimum-energy APS among all covariance-consistent spectra.

Precise Analysis of Covariance Identifiability for Activity Detection in Grant-Free Random Access

We consider the identifiability issue of maximum likelihood based activity detection in massive MIMO based grant-free random access. A prior work by Chen et al. indicates that the identifiability undergoes a phase transition for commonly-used random signatures. In this paper, we provide an analytical characterization of the boundary of the phase transition curve. Our theoretical results agree well with the numerical experiments.

Receiver Design for MIMO Unsourced Random Access with SKP Coding

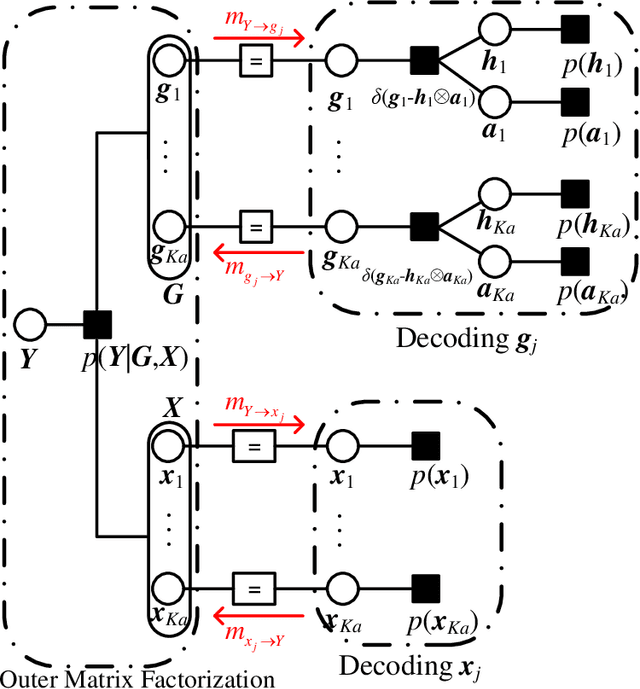
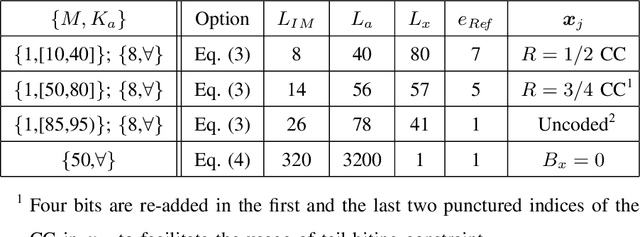
In this letter, we extend the sparse Kronecker-product (SKP) coding scheme, originally designed for the additive white Gaussian noise (AWGN) channel, to multiple input multiple output (MIMO) unsourced random access (URA). With the SKP coding adopted for MIMO transmission, we develop an efficient Bayesian iterative receiver design to solve the intended challenging trilinear factorization problem. Numerical results show that the proposed design outperforms the existing counterparts, and that it performs well in all simulated settings with various antenna sizes and active-user numbers.

Sparse Kronecker-Product Coding for Unsourced Multiple Access

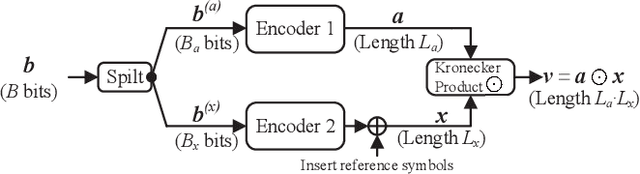
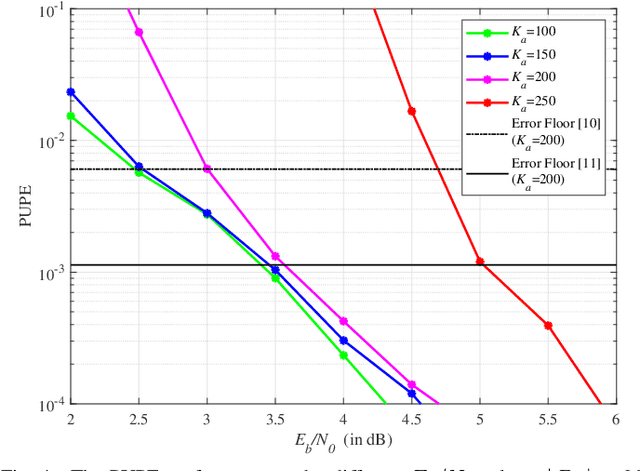
In this paper, a sparse Kronecker-product (SKP) coding scheme is proposed for unsourced multiple access. Specifically, the data of each active user is encoded as the Kronecker product of two component codewords with one being sparse and the other being forward-error-correction (FEC) coded. At the receiver, an iterative decoding algorithm is developed, consisting of matrix factorization for the decomposition of the Kronecker product and soft-in soft-out decoding for the component sparse code and the FEC code. The cyclic redundancy check (CRC) aided interference cancelation technique is further incorporated for performance improvement. Numerical results show that the proposed scheme outperforms the state-of-the-art counterparts, and approaches the random coding bound within a gap of only 0.1 dB at the code length of 30000 when the number of active users is less than 75, and the error rate can be made much lower than the existing schemes, especially when the number of active users is relatively large.

Regularized Recovery by Multi-order Partial Hypergraph Total Variation

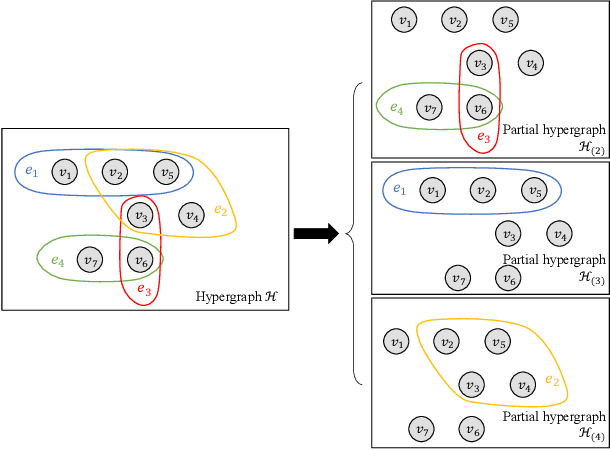
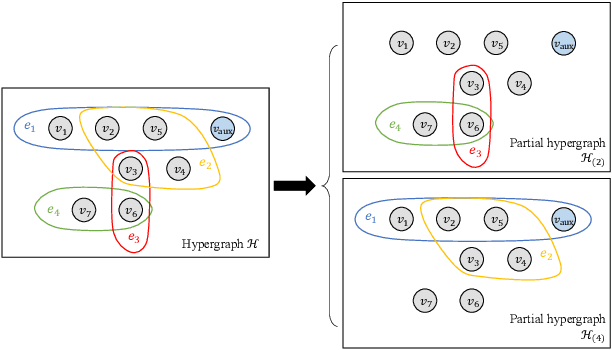
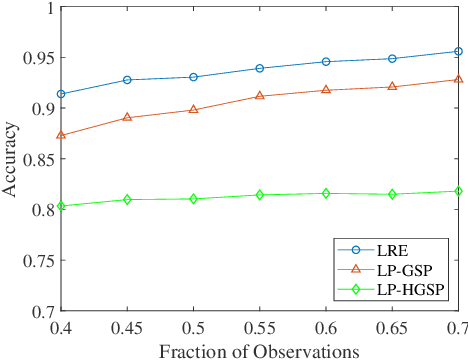
Capturing complex high-order interactions among data is an important task in many scenarios. A common way to model high-order interactions is to use hypergraphs whose topology can be mathematically represented by tensors. Existing methods use a fixed-order tensor to describe the topology of the whole hypergraph, which ignores the divergence of different-order interactions. In this work, we take this divergence into consideration, and propose a multi-order hypergraph Laplacian and the corresponding total variation. Taking this total variation as a regularization term, we can utilize the topology information contained by it to smooth the hypergraph signal. This can help distinguish different-order interactions and represent high-order interactions accurately.