Regularized Recovery by Multi-order Partial Hypergraph Total Variation
Paper and Code
Feb 19, 2021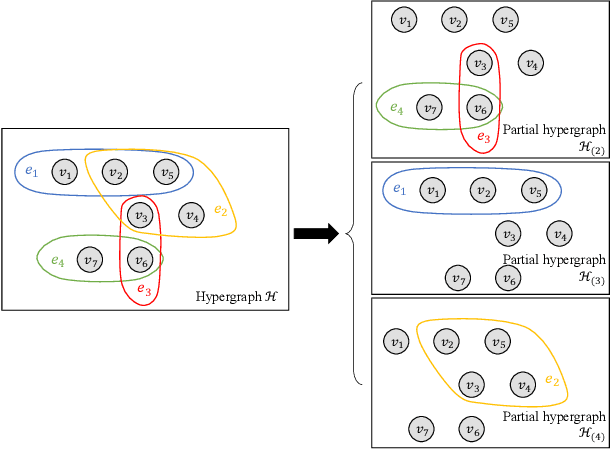
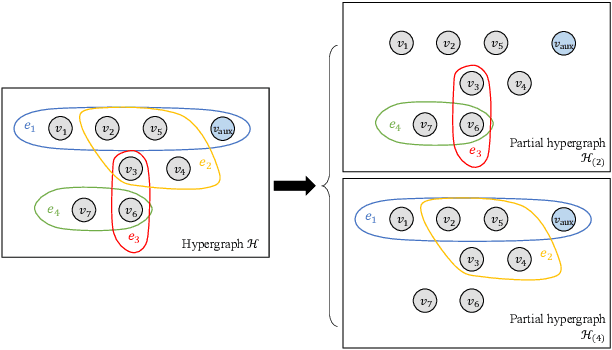
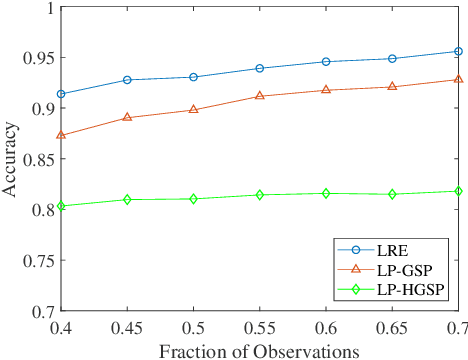
Capturing complex high-order interactions among data is an important task in many scenarios. A common way to model high-order interactions is to use hypergraphs whose topology can be mathematically represented by tensors. Existing methods use a fixed-order tensor to describe the topology of the whole hypergraph, which ignores the divergence of different-order interactions. In this work, we take this divergence into consideration, and propose a multi-order hypergraph Laplacian and the corresponding total variation. Taking this total variation as a regularization term, we can utilize the topology information contained by it to smooth the hypergraph signal. This can help distinguish different-order interactions and represent high-order interactions accurately.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge