Chengze Ye
Learning Wavelet-Sparse FDK for 3D Cone-Beam CT Reconstruction
May 19, 2025Abstract:Cone-Beam Computed Tomography (CBCT) is essential in medical imaging, and the Feldkamp-Davis-Kress (FDK) algorithm is a popular choice for reconstruction due to its efficiency. However, FDK is susceptible to noise and artifacts. While recent deep learning methods offer improved image quality, they often increase computational complexity and lack the interpretability of traditional methods. In this paper, we introduce an enhanced FDK-based neural network that maintains the classical algorithm's interpretability by selectively integrating trainable elements into the cosine weighting and filtering stages. Recognizing the challenge of a large parameter space inherent in 3D CBCT data, we leverage wavelet transformations to create sparse representations of the cosine weights and filters. This strategic sparsification reduces the parameter count by $93.75\%$ without compromising performance, accelerates convergence, and importantly, maintains the inference computational cost equivalent to the classical FDK algorithm. Our method not only ensures volumetric consistency and boosts robustness to noise, but is also designed for straightforward integration into existing CT reconstruction pipelines. This presents a pragmatic enhancement that can benefit clinical applications, particularly in environments with computational limitations.
Filter2Noise: Interpretable Self-Supervised Single-Image Denoising for Low-Dose CT with Attention-Guided Bilateral Filtering
Apr 18, 2025Abstract:Effective denoising is crucial in low-dose CT to enhance subtle structures and low-contrast lesions while preventing diagnostic errors. Supervised methods struggle with limited paired datasets, and self-supervised approaches often require multiple noisy images and rely on deep networks like U-Net, offering little insight into the denoising mechanism. To address these challenges, we propose an interpretable self-supervised single-image denoising framework -- Filter2Noise (F2N). Our approach introduces an Attention-Guided Bilateral Filter that adapted to each noisy input through a lightweight module that predicts spatially varying filter parameters, which can be visualized and adjusted post-training for user-controlled denoising in specific regions of interest. To enable single-image training, we introduce a novel downsampling shuffle strategy with a new self-supervised loss function that extends the concept of Noise2Noise to a single image and addresses spatially correlated noise. On the Mayo Clinic 2016 low-dose CT dataset, F2N outperforms the leading self-supervised single-image method (ZS-N2N) by 4.59 dB PSNR while improving transparency, user control, and parametric efficiency. These features provide key advantages for medical applications that require precise and interpretable noise reduction. Our code is demonstrated at https://github.com/sypsyp97/Filter2Noise.git .
Compressibility Analysis for the differentiable shift-variant Filtered Backprojection Model
Jan 20, 2025



Abstract:The differentiable shift-variant filtered backprojection (FBP) model enables the reconstruction of cone-beam computed tomography (CBCT) data for any non-circular trajectories. This method employs deep learning technique to estimate the redundancy weights required for reconstruction, given knowledge of the specific trajectory at optimization time. However, computing the redundancy weight for each projection remains computationally intensive. This paper presents a novel approach to compress and optimize the differentiable shift-variant FBP model based on Principal Component Analysis (PCA). We apply PCA to the redundancy weights learned from sinusoidal trajectory projection data, revealing significant parameter redundancy in the original model. By integrating PCA directly into the differentiable shift-variant FBP reconstruction pipeline, we develop a method that decomposes the redundancy weight layer parameters into a trainable eigenvector matrix, compressed weights, and a mean vector. This innovative technique achieves a remarkable 97.25% reduction in trainable parameters without compromising reconstruction accuracy. As a result, our algorithm significantly decreases the complexity of the differentiable shift-variant FBP model and greatly improves training speed. These improvements make the model substantially more practical for real-world applications.
DRACO: Differentiable Reconstruction for Arbitrary CBCT Orbits
Oct 18, 2024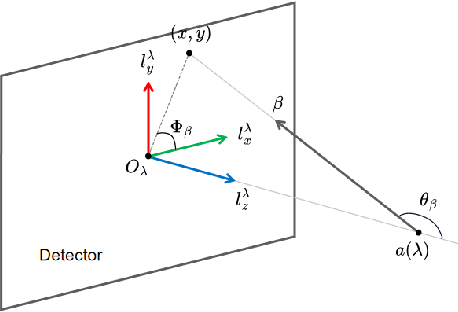


Abstract:This paper introduces a novel method for reconstructing cone beam computed tomography (CBCT) images for arbitrary orbits using a differentiable shift-variant filtered backprojection (FBP) neural network. Traditional CBCT reconstruction methods for arbitrary orbits, like iterative reconstruction algorithms, are computationally expensive and memory-intensive. The proposed method addresses these challenges by employing a shift-variant FBP algorithm optimized for arbitrary trajectories through a deep learning approach that adapts to a specific orbit geometry. This approach overcomes the limitations of existing techniques by integrating known operators into the learning model, minimizing the number of parameters, and improving the interpretability of the model. The proposed method is a significant advancement in interventional medical imaging, particularly for robotic C-arm CT systems, enabling faster and more accurate CBCT reconstructions with customized orbits. Especially this method can also be used for the analytical reconstruction of non-continuous orbits like circular plus arc. The experimental results demonstrate that the proposed method significantly accelerates the reconstruction process compared to conventional iterative algorithms. It achieves comparable or superior image quality, as evidenced by metrics such as the mean squared error (MSE), the peak signal-to-noise ratio (PSNR), and the structural similarity index measure (SSIM). The validation experiments show that the method can handle data from different trajectories, demonstrating its flexibility and robustness across different scan geometries. Our method demonstrates a significant improvement, particularly for the sinusoidal trajectory, achieving a 38.6% reduction in MSE, a 7.7% increase in PSNR, and a 5.0% improvement in SSIM. Furthermore, the computation time for reconstruction was reduced by more than 97%.
Deep Learning Computed Tomography based on the Defrise and Clack Algorithm
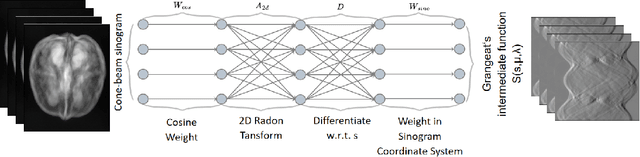
Mar 01, 2024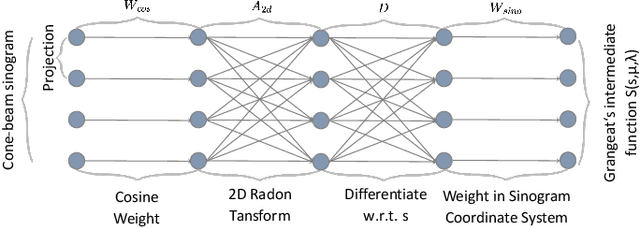
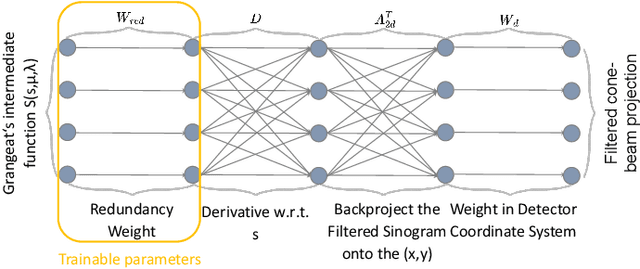

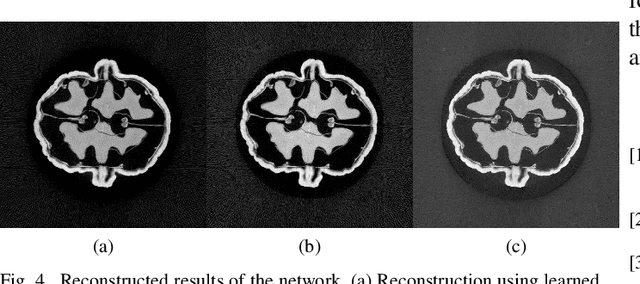
Abstract:This study presents a novel approach for reconstructing cone beam computed tomography (CBCT) for specific orbits using known operator learning. Unlike traditional methods, this technique employs a filtered backprojection type (FBP-type) algorithm, which integrates a unique, adaptive filtering process. This process involves a series of operations, including weightings, differentiations, the 2D Radon transform, and backprojection. The filter is designed for a specific orbit geometry and is obtained using a data-driven approach based on deep learning. The approach efficiently learns and optimizes the orbit-related component of the filter. The method has demonstrated its ability through experimentation by successfully learning parameters from circular orbit projection data. Subsequently, the optimized parameters are used to reconstruct images, resulting in outcomes that closely resemble the analytical solution. This demonstrates the potential of the method to learn appropriate parameters from any specific orbit projection data and achieve reconstruction. The algorithm has demonstrated improvement, particularly in enhancing reconstruction speed and reducing memory usage for handling specific orbit reconstruction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge