Efficient Ridge Solutions for the Incremental Broad Learning System on Added Inputs by Updating the Inverse or the Inverse Cholesky Factor of the Hermitian matrix in the Ridge Inverse

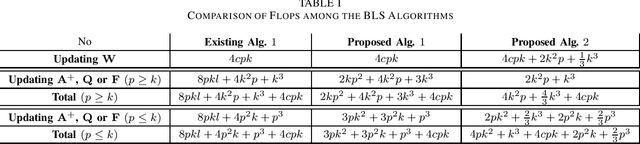
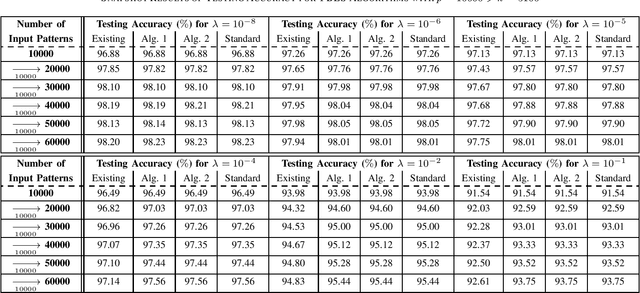
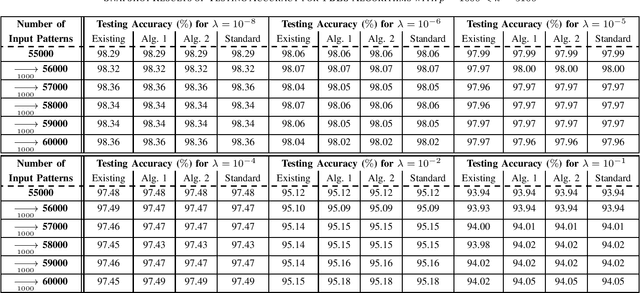
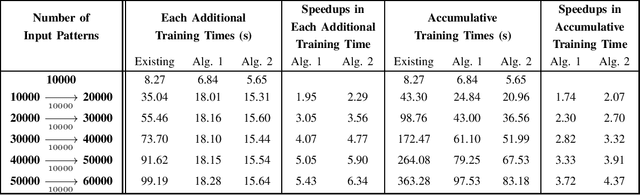
This brief proposes two BLS algorithms to improve the existing BLS for new added inputs in [7]. The proposed BLS algorithms avoid computing the ridge inverse, by computing the ridge solution (i.e., the output weights) from the inverse or the inverse Cholesky factor of the Hermitian matrix in the ridge inverse. The proposed BLS algorithm 1 updates the inverse of the Hermitian matrix by the matrix inversion lemma [12]. To update the upper-triangular inverse Cholesky factor of the Hermitian matrix, the proposed BLS algorithm 2 multiplies the inverse Cholesky factor with an upper-triangular intermediate matrix, which is computed by a Cholesky factorization or an inverse Cholesky factorization. Assume that the newly added input matrix corresponding to the added inputs is p * k, where p and k are the number of added training samples and the total node number, respectively. When p > k, the inverse of a sum of matrices [11] is utilized to compute the intermediate variables by a smaller matrix inverse in the proposed algorithm 1, or by a smaller inverse Cholesky factorization in the proposed algorithm 2. Usually the Hermitian matrix in the ridge inverse is smaller than the ridge inverse. Thus the proposed algorithms 1 and 2 require less flops (floating-point operations) than the existing BLS algorithm, which is verified by the theoretical flops calculation. In numerical experiments, the speedups for the case of p > k in each additional training time of the proposed BLS algorithms 1 and 2 over the existing algorithm are 1.95 - 5.43 and 2.29 - 6.34, respectively, and the speedups for the case of p < k are 8.83 - 10.21 and 2.28 - 2.58, respectively.

Efficient Ridge Solution for the Incremental Broad Learning System on Added Nodes by Inverse Cholesky Factorization of a Partitioned Matrix

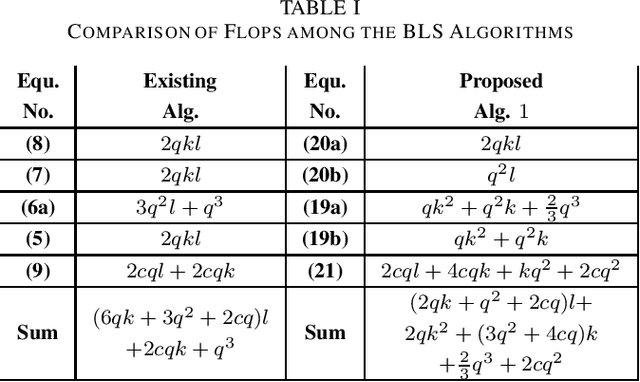
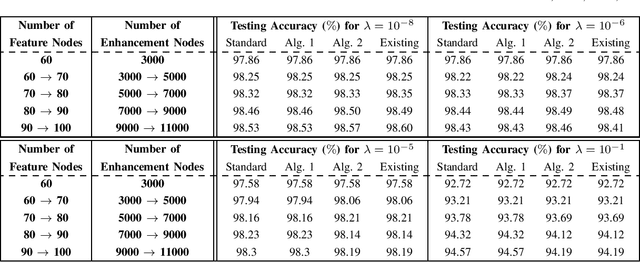
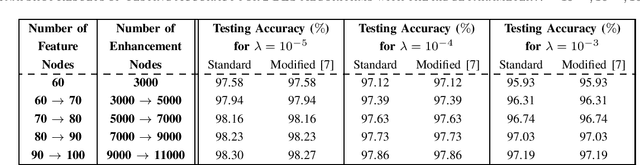
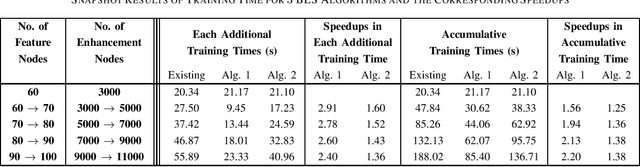
To accelerate the existing Broad Learning System (BLS) for new added nodes in [7], we extend the inverse Cholesky factorization in [10] to deduce an efficient inverse Cholesky factorization for a Hermitian matrix partitioned into 2 * 2 blocks, which is utilized to develop the proposed BLS algorithm 1. The proposed BLS algorithm 1 compute the ridge solution (i.e, the output weights) from the inverse Cholesky factor of the Hermitian matrix in the ridge inverse, and update the inverse Cholesky factor efficiently. From the proposed BLS algorithm 1, we deduce the proposed ridge inverse, which can be obtained from the generalized inverse in [7] by just change one matrix in the equation to compute the newly added sub-matrix. We also modify the proposed algorithm 1 into the proposed algorithm 2, which is equivalent to the existing BLS algorithm [7] in terms of numerical computations. The proposed algorithms 1 and 2 can reduce the computational complexity, since usually the Hermitian matrix in the ridge inverse is smaller than the ridge inverse. With respect to the existing BLS algorithm, the proposed algorithms 1 and 2 usually require about 13 and 2 3 of complexities, respectively, while in numerical experiments they achieve the speedups (in each additional training time) of 2.40 - 2.91 and 1.36 - 1.60, respectively. Numerical experiments also show that the proposed algorithm 1 and the standard ridge solution always bear the same testing accuracy, and usually so do the proposed algorithm 2 and the existing BLS algorithm. The existing BLS assumes the ridge parameter lamda->0, since it is based on the generalized inverse with the ridge regression approximation. When the assumption of lamda-> 0 is not satisfied, the standard ridge solution obviously achieves a better testing accuracy than the existing BLS algorithm in numerical experiments.

Efficient Inverse-Free Algorithms for Extreme Learning Machine Based on the Recursive Matrix Inverse and the Inverse LDL' Factorization

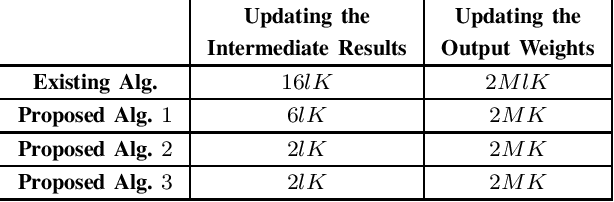
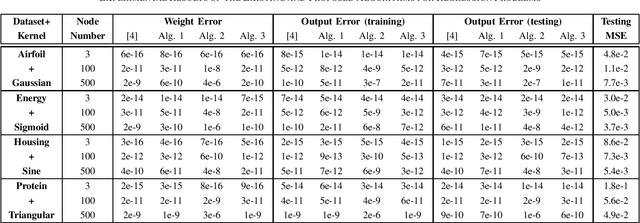
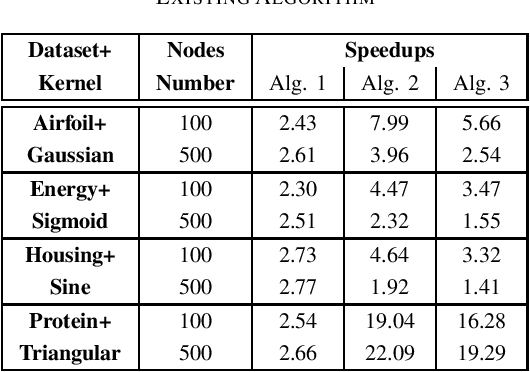
The inverse-free extreme learning machine (ELM) algorithm proposed in [4] was based on an inverse-free algorithm to compute the regularized pseudo-inverse, which was deduced from an inverse-free recursive algorithm to update the inverse of a Hermitian matrix. Before that recursive algorithm was applied in [4], its improved version had been utilized in previous literatures [9], [10]. Accordingly from the improved recursive algorithm [9], [10], we deduce a more efficient inverse-free algorithm to update the regularized pseudo-inverse, from which we develop the proposed inverse-free ELM algorithm 1. Moreover, the proposed ELM algorithm 2 further reduces the computational complexity, which computes the output weights directly from the updated inverse, and avoids computing the regularized pseudoinverse. Lastly, instead of updating the inverse, the proposed ELM algorithm 3 updates the LDLT factor of the inverse by the inverse LDLT factorization [11], to avoid numerical instabilities after a very large number of iterations [12]. With respect to the existing ELM algorithm, the proposed ELM algorithms 1, 2 and 3 are expected to require only (8+3)/M , (8+1)/M and (8+1)/M of complexities, respectively, where M is the output node number. In the numerical experiments, the standard ELM, the existing inverse-free ELM algorithm and the proposed ELM algorithms 1, 2 and 3 achieve the same performance in regression and classification, while all the 3 proposed algorithms significantly accelerate the existing inverse-free ELM algorithm

Reducing the Computational Complexity of Pseudoinverse for the Incremental Broad Learning System on Added Inputs

In this brief, we improve the Broad Learning System (BLS) [7] by reducing the computational complexity of the incremental learning for added inputs. We utilize the inverse of a sum of matrices in [8] to improve a step in the pseudoinverse of a row-partitioned matrix. Accordingly we propose two fast algorithms for the cases of q > k and q < k, respectively, where q and k denote the number of additional training samples and the total number of nodes, respectively. Specifically, when q > k, the proposed algorithm computes only a k * k matrix inverse, instead of a q * q matrix inverse in the existing algorithm. Accordingly it can reduce the complexity dramatically. Our simulations, which follow those for Table V in [7], show that the proposed algorithm and the existing algorithm achieve the same testing accuracy, while the speedups in BLS training time of the proposed algorithm over the existing algorithm are 1.24 - 1.30.

A Random Sample Partition Data Model for Big Data Analysis

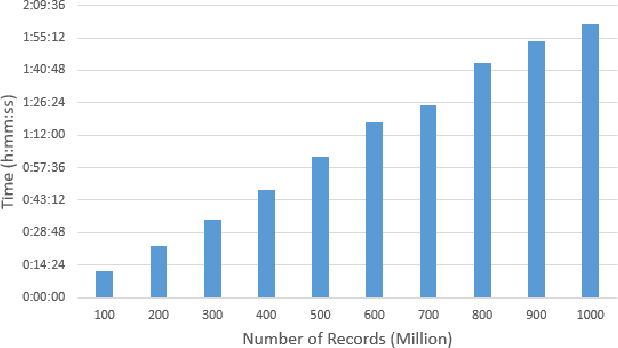
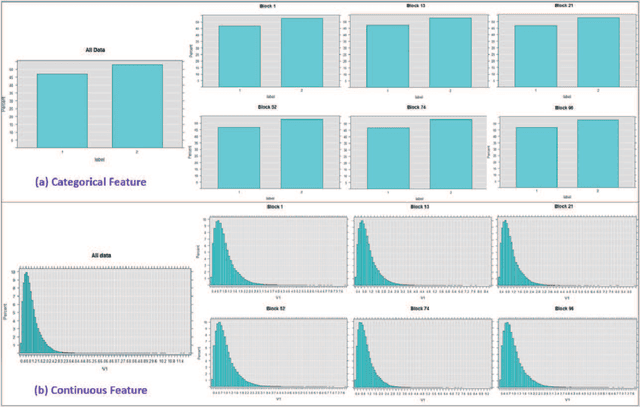
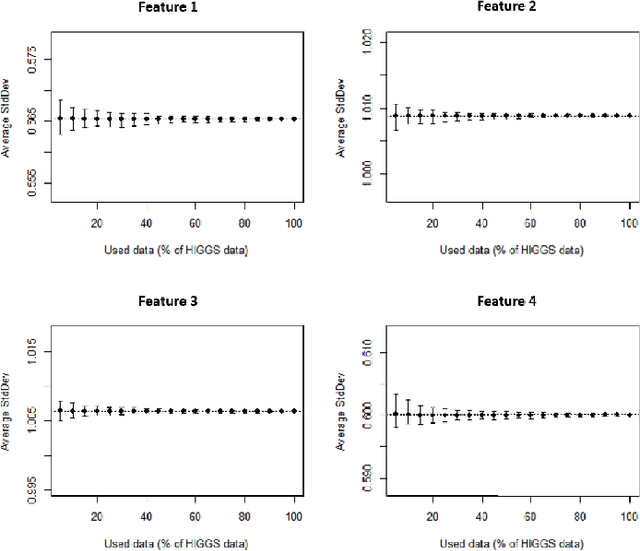
Big data sets must be carefully partitioned into statistically similar data subsets that can be used as representative samples for big data analysis tasks. In this paper, we propose the random sample partition (RSP) data model to represent a big data set as a set of non-overlapping data subsets, called RSP data blocks, where each RSP data block has a probability distribution similar to the whole big data set. Under this data model, efficient block level sampling is used to randomly select RSP data blocks, replacing expensive record level sampling to select sample data from a big distributed data set on a computing cluster. We show how RSP data blocks can be employed to estimate statistics of a big data set and build models which are equivalent to those built from the whole big data set. In this approach, analysis of a big data set becomes analysis of few RSP data blocks which have been generated in advance on the computing cluster. Therefore, the new method for data analysis based on RSP data blocks is scalable to big data.