Recursive LMMSE-Based Iterative Soft Interference Cancellation for MIMO Systems to Save Computations and Memories

Firstly, a reordered description is given for the linear minimum mean square error (LMMSE)-based iterative soft interference cancellation (ISIC) detection process for Mutipleinput multiple-output (MIMO) wireless communication systems, which is based on the equivalent channel matrix. Then the above reordered description is applied to compare the detection process for LMMSE-ISIC with that for the hard decision (HD)-based ordered successive interference cancellation (OSIC) scheme, to draw the conclusion that the former is the extension of the latter. Finally, the recursive scheme for HD-OSIC with reduced complexity and memory saving is extended to propose the recursive scheme for LMMSE-ISIC, where the required computations and memories are reduced by computing the filtering bias and the estimate from the Hermitian inverse matrix and the symbol estimate vector, and updating the Hermitian inverse matrix and the symbol estimate vector efficiently. Assume N transmitters and M (no less than N) receivers in the MIMO system. Compared to the existing low-complexity LMMSE-ISIC scheme, the proposed recursive LMMSE-ISIC scheme requires no more than 1/6 computations and no more than 1/5 memory units.

Improved Recursive Algorithms for V-BLAST to Reduce the Complexity and Save Memories

Improvements I-IV were proposed to reduce the computational complexity of the original recursive algorithm for vertical Bell Laboratories layered space-time architecture (VBLAST). The existing recursive algorithm with speed advantage and that with memory saving incorporate Improvements I-IV and only Improvements III-IV into the original algorithm, respectively. To the best of our knowledge, the algorithm with speed advantage and that with memory saving require the lowest complexity and the least memories, respectively, among the existing recursive V-BLAST algorithms. We propose Improvements V and VI to replace Improvements I and II, respectively. Instead of the lemma for inversion of partitioned matrix applied in Improvement I, Improvement V uses another lemma to speed up the matrix inversion step by the factor of 1.67. Then the formulas adopted in our Improvement V are applied to deduce Improvement VI, which includes the improved interference cancellation scheme with memory saving. In the existing algorithm with speed advantage, the proposed algorithm I with speed advantage replaces Improvement I with Improvement V, while the proposed algorithm II with both speed advantage and memory saving replaces Improvements I and II with Improvements V and VI, respectively. Both proposed algorithms speed up the existing algorithm with speed advantage by the factor of 1.3, while the proposed algorithm II achieves the speedup of 1.86 and saves about half memories, compared to the existing algorithm with memory saving.

Low-Memory Implementations of Ridge Solutions for Broad Learning System with Incremental Learning

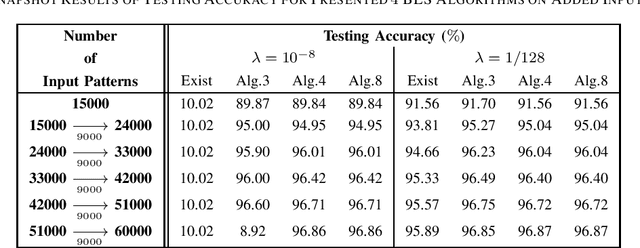
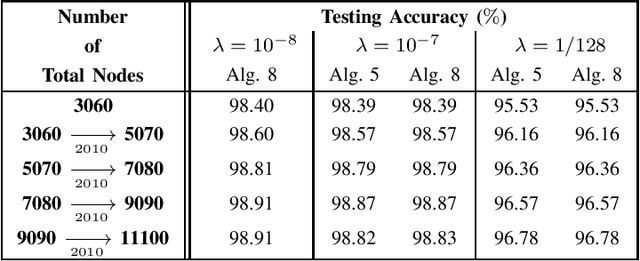
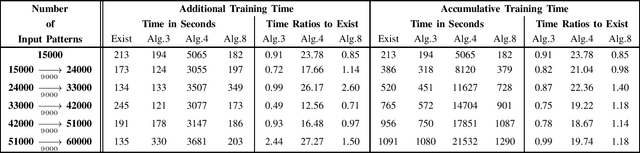
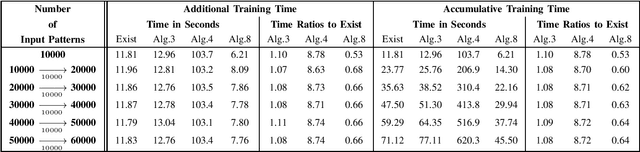
The existing low-memory BLS implementation proposed recently avoids the need for storing and inverting large matrices, to achieve efficient usage of memories. However, the existing low-memory BLS implementation sacrifices the testing accuracy as a price for efficient usage of memories, since it can no longer obtain the generalized inverse or ridge solution for the output weights during incremental learning, and it cannot work under the very small ridge parameter that is utilized in the original BLS. Accordingly, it is required to develop the low-memory BLS implementations, which can work under very small ridge parameters and compute the generalized inverse or ridge solution for the output weights in the process of incremental learning. In this paper, firstly we propose the low-memory implementations for the recently proposed recursive and square-root BLS algorithms on added inputs and the recently proposed squareroot BLS algorithm on added nodes, by simply processing a batch of inputs or nodes in each recursion. Since the recursive BLS implementation includes the recursive updates of the inverse matrix that may introduce numerical instabilities after a large number of iterations, and needs the extra computational load to decompose the inverse matrix into the Cholesky factor when cooperating with the proposed low-memory implementation of the square-root BLS algorithm on added nodes, we only improve the low-memory implementations of the square-root BLS algorithms on added inputs and nodes, to propose the full lowmemory implementation of the square-root BLS algorithm. All the proposed low-memory BLS implementations compute the ridge solution for the output weights in the process of incremental learning, and most of them can work under very small ridge parameters.

Efficient and Stable Algorithms to Extend Greville's Method to Partitioned Matrices Based on Inverse Cholesky Factorization

Greville's method has been utilized in (Broad Learn-ing System) BLS to propose an effective and efficient incremental learning system without retraining the whole network from the beginning. For a column-partitioned matrix where the second part consists of p columns, Greville's method requires p iterations to compute the pseudoinverse of the whole matrix from the pseudoinverse of the first part. The incremental algorithms in BLS extend Greville's method to compute the pseudoinverse of the whole matrix from the pseudoinverse of the first part by just 1 iteration, which have neglected some possible cases, and need further improvements in efficiency and numerical stability. In this paper, we propose an efficient and numerical stable algorithm from Greville's method, to compute the pseudoinverse of the whole matrix from the pseudoinverse of the first part by just 1 iteration, where all possible cases are considered, and the recently proposed inverse Cholesky factorization can be applied to further reduce the computational complexity. Finally, we give the whole algorithm for column-partitioned matrices in BLS. On the other hand, we also give the proposed algorithm for row-partitioned matrices in BLS.

Efficient Inverse-Free Incremental and Decremental Algorithms for Multiple Hidden Nodes in Extreme Learning Machine

The inverse-free extreme learning machine (ELM) algorithm proposed in [4] was based on an inverse-free algorithm to compute the regularized pseudo-inverse, which was deduced from an inverse-free recursive algorithm to update the inverse of a Hermitian matrix. Before that recursive algorithm was applied in [4], its improved version had been utilized in previous literatures [9], [10]. Accordingly from the improved recursive algorithm [9], [10], several efficient inverse-free algorithms for ELM were proposed in [13] to reduce the computational complexity. In this paper, we propose two inverse-free algorithms for ELM with Tikhonov regularization, which can increase multiple hidden nodes in an iteration. On the other hand, we also propose two efficient decremental learning algorithms for ELM with Tikhonov regularization, which can remove multiple redundant nodes in an iteration.

Efficient Decremental Learning Algorithms for Broad Learning System

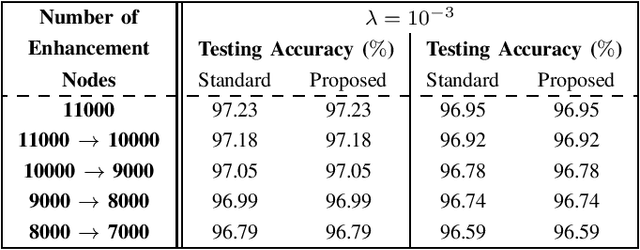
The decremented learning algorithms are required in machine learning, to prune redundant nodes and remove obsolete inline training samples. In this paper, an efficient decremented learning algorithm to prune redundant nodes is deduced from the incremental learning algorithm 1 proposed in [9] for added nodes, and two decremented learning algorithms to remove training samples are deduced from the two incremental learning algorithms proposed in [10] for added inputs. The proposed decremented learning algorithm for reduced nodes utilizes the inverse Cholesterol factor of the Herminia matrix in the ridge inverse, to update the output weights recursively, as the incremental learning algorithm 1 for added nodes in [9], while that inverse Cholesterol factor is updated with an unitary transformation. The proposed decremented learning algorithm 1 for reduced inputs updates the output weights recursively with the inverse of the Herminia matrix in the ridge inverse, and updates that inverse recursively, as the incremental learning algorithm 1 for added inputs in [10].

Efficient Ridge Solutions for the Incremental Broad Learning System on Added Inputs by Updating the Inverse or the Inverse Cholesky Factor of the Hermitian matrix in the Ridge Inverse

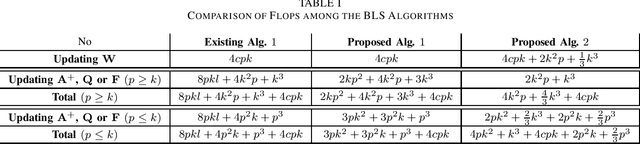
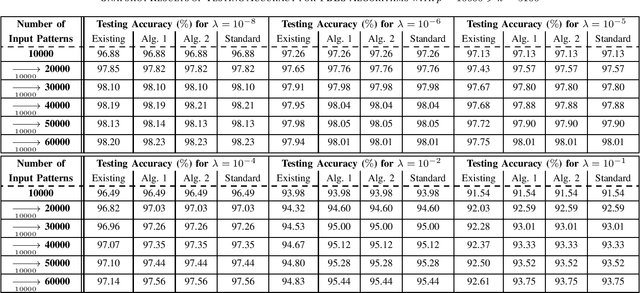
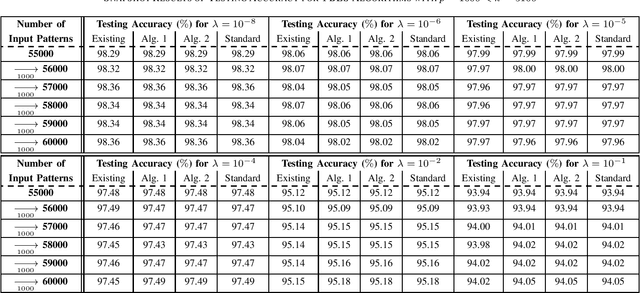
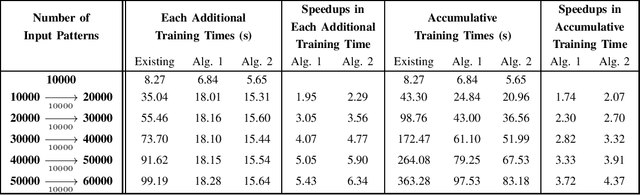
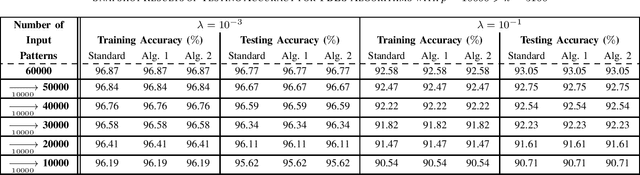
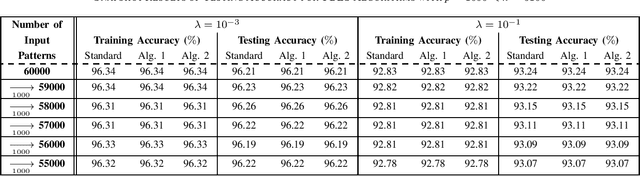
This brief proposes two BLS algorithms to improve the existing BLS for new added inputs in [7]. The proposed BLS algorithms avoid computing the ridge inverse, by computing the ridge solution (i.e., the output weights) from the inverse or the inverse Cholesky factor of the Hermitian matrix in the ridge inverse. The proposed BLS algorithm 1 updates the inverse of the Hermitian matrix by the matrix inversion lemma [12]. To update the upper-triangular inverse Cholesky factor of the Hermitian matrix, the proposed BLS algorithm 2 multiplies the inverse Cholesky factor with an upper-triangular intermediate matrix, which is computed by a Cholesky factorization or an inverse Cholesky factorization. Assume that the newly added input matrix corresponding to the added inputs is p * k, where p and k are the number of added training samples and the total node number, respectively. When p > k, the inverse of a sum of matrices [11] is utilized to compute the intermediate variables by a smaller matrix inverse in the proposed algorithm 1, or by a smaller inverse Cholesky factorization in the proposed algorithm 2. Usually the Hermitian matrix in the ridge inverse is smaller than the ridge inverse. Thus the proposed algorithms 1 and 2 require less flops (floating-point operations) than the existing BLS algorithm, which is verified by the theoretical flops calculation. In numerical experiments, the speedups for the case of p > k in each additional training time of the proposed BLS algorithms 1 and 2 over the existing algorithm are 1.95 - 5.43 and 2.29 - 6.34, respectively, and the speedups for the case of p < k are 8.83 - 10.21 and 2.28 - 2.58, respectively.

Efficient Ridge Solution for the Incremental Broad Learning System on Added Nodes by Inverse Cholesky Factorization of a Partitioned Matrix

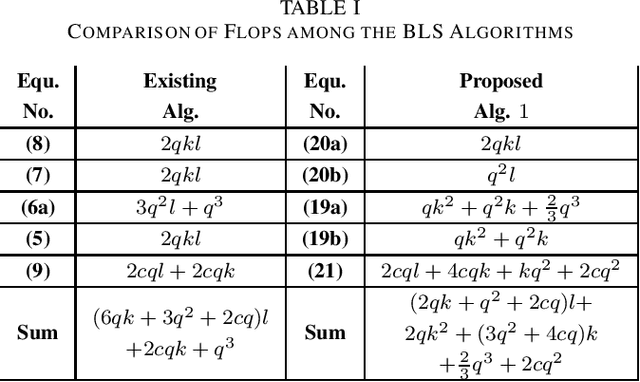
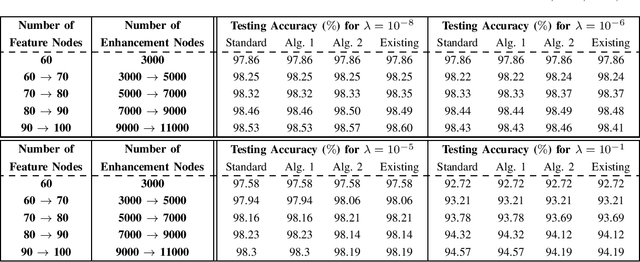
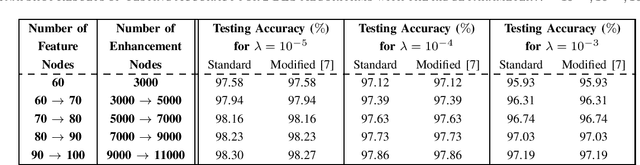
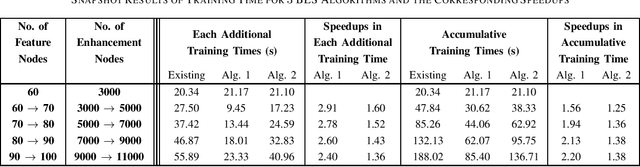
To accelerate the existing Broad Learning System (BLS) for new added nodes in [7], we extend the inverse Cholesky factorization in [10] to deduce an efficient inverse Cholesky factorization for a Hermitian matrix partitioned into 2 * 2 blocks, which is utilized to develop the proposed BLS algorithm 1. The proposed BLS algorithm 1 compute the ridge solution (i.e, the output weights) from the inverse Cholesky factor of the Hermitian matrix in the ridge inverse, and update the inverse Cholesky factor efficiently. From the proposed BLS algorithm 1, we deduce the proposed ridge inverse, which can be obtained from the generalized inverse in [7] by just change one matrix in the equation to compute the newly added sub-matrix. We also modify the proposed algorithm 1 into the proposed algorithm 2, which is equivalent to the existing BLS algorithm [7] in terms of numerical computations. The proposed algorithms 1 and 2 can reduce the computational complexity, since usually the Hermitian matrix in the ridge inverse is smaller than the ridge inverse. With respect to the existing BLS algorithm, the proposed algorithms 1 and 2 usually require about 13 and 2 3 of complexities, respectively, while in numerical experiments they achieve the speedups (in each additional training time) of 2.40 - 2.91 and 1.36 - 1.60, respectively. Numerical experiments also show that the proposed algorithm 1 and the standard ridge solution always bear the same testing accuracy, and usually so do the proposed algorithm 2 and the existing BLS algorithm. The existing BLS assumes the ridge parameter lamda->0, since it is based on the generalized inverse with the ridge regression approximation. When the assumption of lamda-> 0 is not satisfied, the standard ridge solution obviously achieves a better testing accuracy than the existing BLS algorithm in numerical experiments.

Efficient Inverse-Free Algorithms for Extreme Learning Machine Based on the Recursive Matrix Inverse and the Inverse LDL' Factorization

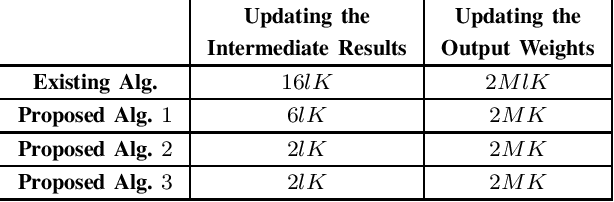
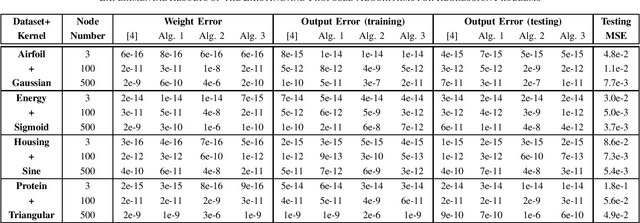
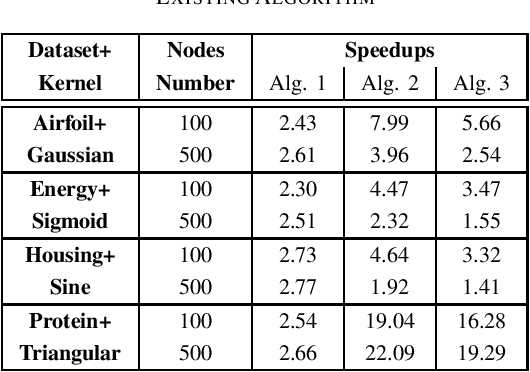
The inverse-free extreme learning machine (ELM) algorithm proposed in [4] was based on an inverse-free algorithm to compute the regularized pseudo-inverse, which was deduced from an inverse-free recursive algorithm to update the inverse of a Hermitian matrix. Before that recursive algorithm was applied in [4], its improved version had been utilized in previous literatures [9], [10]. Accordingly from the improved recursive algorithm [9], [10], we deduce a more efficient inverse-free algorithm to update the regularized pseudo-inverse, from which we develop the proposed inverse-free ELM algorithm 1. Moreover, the proposed ELM algorithm 2 further reduces the computational complexity, which computes the output weights directly from the updated inverse, and avoids computing the regularized pseudoinverse. Lastly, instead of updating the inverse, the proposed ELM algorithm 3 updates the LDLT factor of the inverse by the inverse LDLT factorization [11], to avoid numerical instabilities after a very large number of iterations [12]. With respect to the existing ELM algorithm, the proposed ELM algorithms 1, 2 and 3 are expected to require only (8+3)/M , (8+1)/M and (8+1)/M of complexities, respectively, where M is the output node number. In the numerical experiments, the standard ELM, the existing inverse-free ELM algorithm and the proposed ELM algorithms 1, 2 and 3 achieve the same performance in regression and classification, while all the 3 proposed algorithms significantly accelerate the existing inverse-free ELM algorithm

Reducing the Computational Complexity of Pseudoinverse for the Incremental Broad Learning System on Added Inputs

In this brief, we improve the Broad Learning System (BLS) [7] by reducing the computational complexity of the incremental learning for added inputs. We utilize the inverse of a sum of matrices in [8] to improve a step in the pseudoinverse of a row-partitioned matrix. Accordingly we propose two fast algorithms for the cases of q > k and q < k, respectively, where q and k denote the number of additional training samples and the total number of nodes, respectively. Specifically, when q > k, the proposed algorithm computes only a k * k matrix inverse, instead of a q * q matrix inverse in the existing algorithm. Accordingly it can reduce the complexity dramatically. Our simulations, which follow those for Table V in [7], show that the proposed algorithm and the existing algorithm achieve the same testing accuracy, while the speedups in BLS training time of the proposed algorithm over the existing algorithm are 1.24 - 1.30.