Low-Memory Implementations of Ridge Solutions for Broad Learning System with Incremental Learning
Paper and Code
May 24, 2021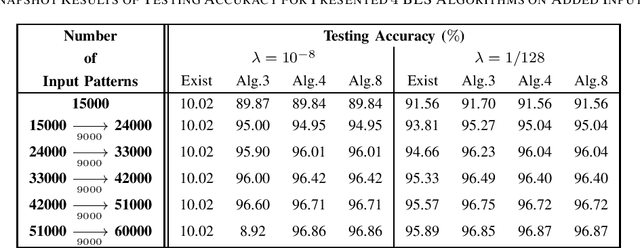
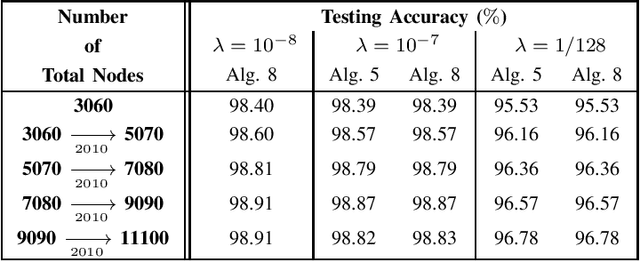
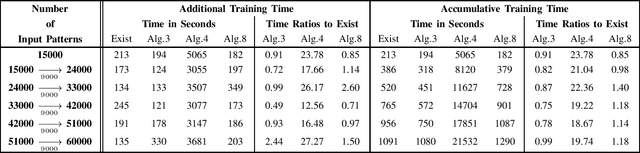
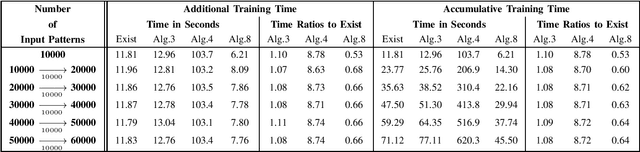
The existing low-memory BLS implementation proposed recently avoids the need for storing and inverting large matrices, to achieve efficient usage of memories. However, the existing low-memory BLS implementation sacrifices the testing accuracy as a price for efficient usage of memories, since it can no longer obtain the generalized inverse or ridge solution for the output weights during incremental learning, and it cannot work under the very small ridge parameter that is utilized in the original BLS. Accordingly, it is required to develop the low-memory BLS implementations, which can work under very small ridge parameters and compute the generalized inverse or ridge solution for the output weights in the process of incremental learning. In this paper, firstly we propose the low-memory implementations for the recently proposed recursive and square-root BLS algorithms on added inputs and the recently proposed squareroot BLS algorithm on added nodes, by simply processing a batch of inputs or nodes in each recursion. Since the recursive BLS implementation includes the recursive updates of the inverse matrix that may introduce numerical instabilities after a large number of iterations, and needs the extra computational load to decompose the inverse matrix into the Cholesky factor when cooperating with the proposed low-memory implementation of the square-root BLS algorithm on added nodes, we only improve the low-memory implementations of the square-root BLS algorithms on added inputs and nodes, to propose the full lowmemory implementation of the square-root BLS algorithm. All the proposed low-memory BLS implementations compute the ridge solution for the output weights in the process of incremental learning, and most of them can work under very small ridge parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge