Efficient Ridge Solutions for the Incremental Broad Learning System on Added Inputs by Updating the Inverse or the Inverse Cholesky Factor of the Hermitian matrix in the Ridge Inverse

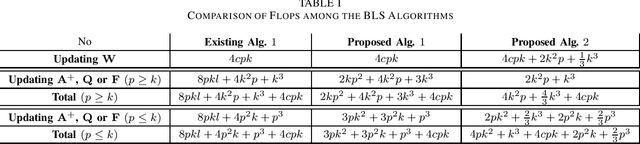
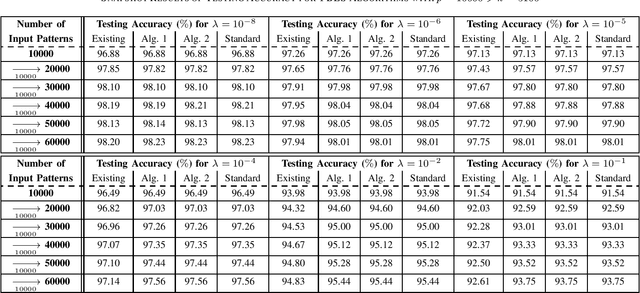
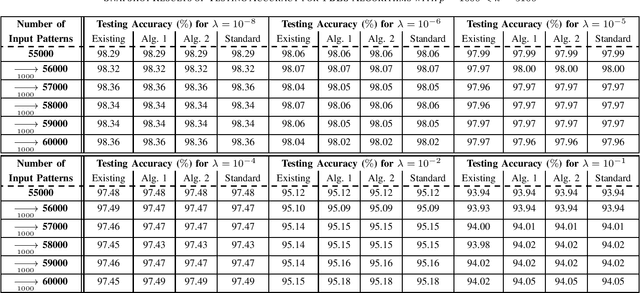
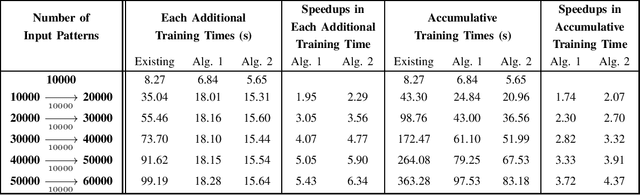
This brief proposes two BLS algorithms to improve the existing BLS for new added inputs in [7]. The proposed BLS algorithms avoid computing the ridge inverse, by computing the ridge solution (i.e., the output weights) from the inverse or the inverse Cholesky factor of the Hermitian matrix in the ridge inverse. The proposed BLS algorithm 1 updates the inverse of the Hermitian matrix by the matrix inversion lemma [12]. To update the upper-triangular inverse Cholesky factor of the Hermitian matrix, the proposed BLS algorithm 2 multiplies the inverse Cholesky factor with an upper-triangular intermediate matrix, which is computed by a Cholesky factorization or an inverse Cholesky factorization. Assume that the newly added input matrix corresponding to the added inputs is p * k, where p and k are the number of added training samples and the total node number, respectively. When p > k, the inverse of a sum of matrices [11] is utilized to compute the intermediate variables by a smaller matrix inverse in the proposed algorithm 1, or by a smaller inverse Cholesky factorization in the proposed algorithm 2. Usually the Hermitian matrix in the ridge inverse is smaller than the ridge inverse. Thus the proposed algorithms 1 and 2 require less flops (floating-point operations) than the existing BLS algorithm, which is verified by the theoretical flops calculation. In numerical experiments, the speedups for the case of p > k in each additional training time of the proposed BLS algorithms 1 and 2 over the existing algorithm are 1.95 - 5.43 and 2.29 - 6.34, respectively, and the speedups for the case of p < k are 8.83 - 10.21 and 2.28 - 2.58, respectively.