Modular Constraint Solver Cooperation via Abstract Interpretation

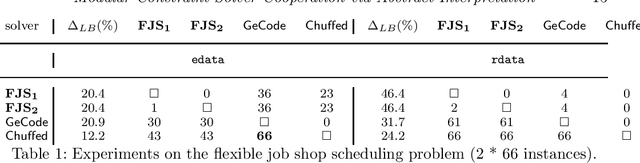
Cooperation among constraint solvers is difficult because different solving paradigms have different theoretical foundations. Recent works have shown that abstract interpretation can provide a unifying theory for various constraint solvers. In particular, it relies on abstract domains which capture constraint languages as ordered structures. The key insight of this paper is viewing cooperation schemes as abstract domains combinations. We propose a modular framework in which solvers and cooperation schemes can be seamlessly added and combined. This differs from existing approaches such as SMT where the cooperation scheme is usually fixed (e.g., Nelson-Oppen). We contribute to two new cooperation schemes: (i) interval propagators completion that allows abstract domains to exchange bound constraints, and (ii) delayed product which exchanges over-approximations of constraints between two abstract domains. Moreover, the delayed product is based on delayed goal of logic programming, and it shows that abstract domains can also capture control aspects of constraint solving. Finally, to achieve modularity, we propose the shared product to combine abstract domains and cooperation schemes. Our approach has been fully implemented, and we provide various examples on the flexible job shop scheduling problem. Under consideration for acceptance in TPLP.

A Probabilistic-Based Model for Binary CSP

This work introduces a probabilistic-based model for binary CSP that provides a fine grained analysis of its internal structure. Assuming that a domain modification could occur in the CSP, it shows how to express, in a predictive way, the probability that a domain value becomes inconsistent, then it express the expectation of the number of arc-inconsistent values in each domain of the constraint network. Thus, it express the expectation of the number of arc-inconsistent values for the whole constraint network. Next, it provides bounds for each of these three probabilistic indicators. Finally, a polytime algorithm, which propagates the probabilistic information, is presented.

Prediction of Parallel Speed-ups for Las Vegas Algorithms

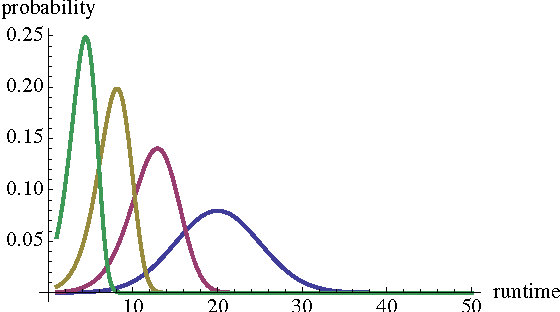
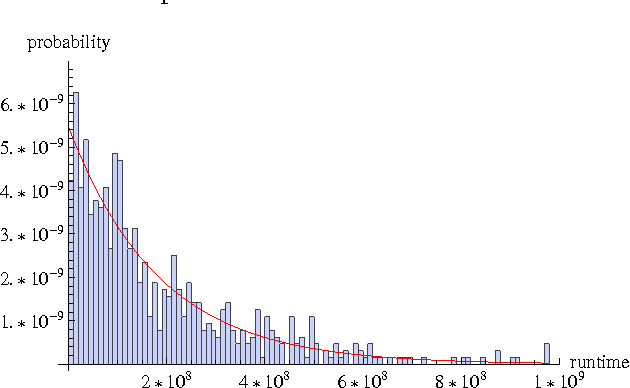
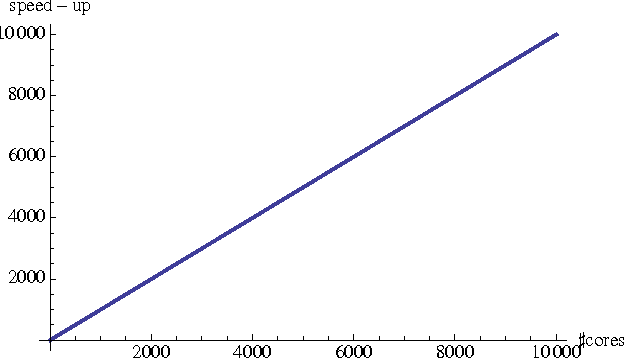
We propose a probabilistic model for the parallel execution of Las Vegas algorithms, i.e., randomized algorithms whose runtime might vary from one execution to another, even with the same input. This model aims at predicting the parallel performances (i.e., speedups) by analysis the runtime distribution of the sequential runs of the algorithm. Then, we study in practice the case of a particular Las Vegas algorithm for combinatorial optimization, on three classical problems, and compare with an actual parallel implementation up to 256 cores. We show that the prediction can be quite accurate, matching the actual speedups very well up to 100 parallel cores and then with a deviation of about 20% up to 256 cores.

Sonet Network Design Problems

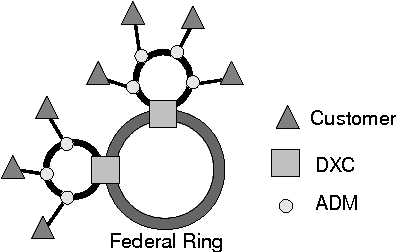
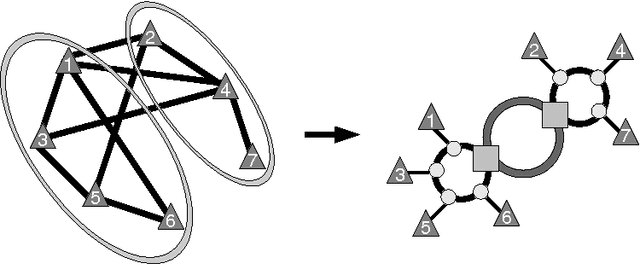
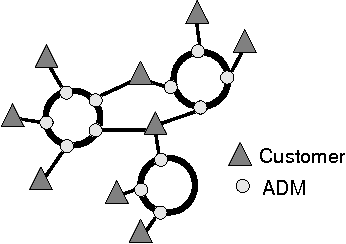
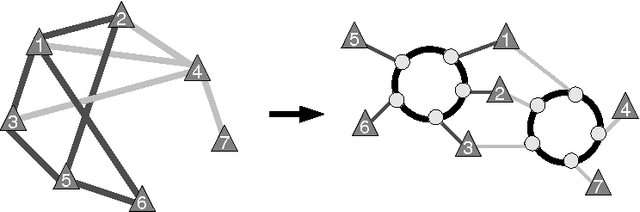
This paper presents a new method and a constraint-based objective function to solve two problems related to the design of optical telecommunication networks, namely the Synchronous Optical Network Ring Assignment Problem (SRAP) and the Intra-ring Synchronous Optical Network Design Problem (IDP). These network topology problems can be represented as a graph partitioning with capacity constraints as shown in previous works. We present here a new objective function and a new local search algorithm to solve these problems. Experiments conducted in Comet allow us to compare our method to previous ones and show that we obtain better results.