Prediction of Parallel Speed-ups for Las Vegas Algorithms
Paper and Code
Dec 18, 2012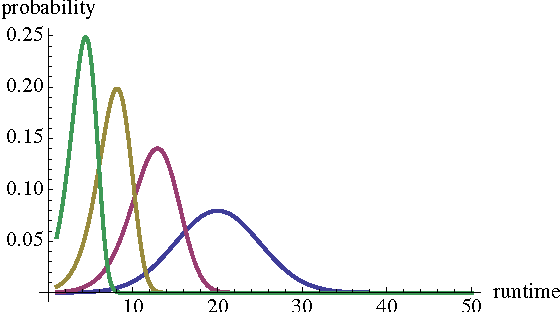

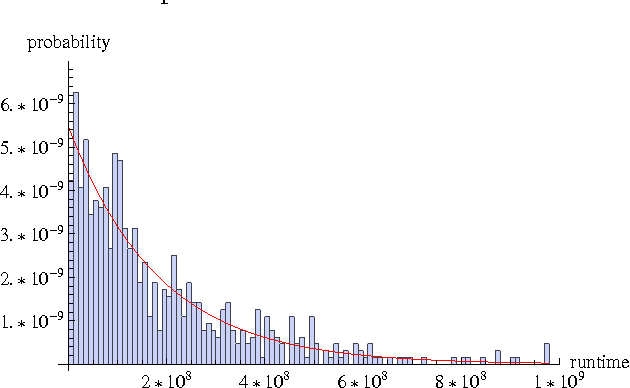
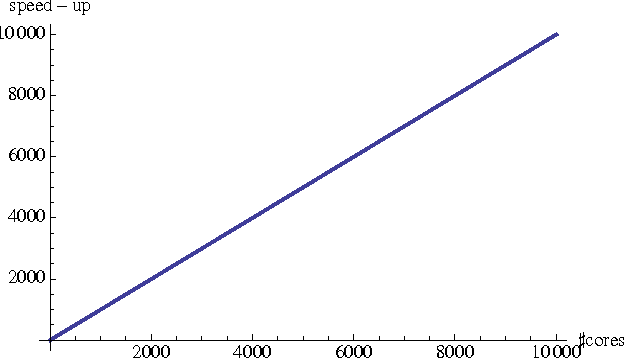
We propose a probabilistic model for the parallel execution of Las Vegas algorithms, i.e., randomized algorithms whose runtime might vary from one execution to another, even with the same input. This model aims at predicting the parallel performances (i.e., speedups) by analysis the runtime distribution of the sequential runs of the algorithm. Then, we study in practice the case of a particular Las Vegas algorithm for combinatorial optimization, on three classical problems, and compare with an actual parallel implementation up to 256 cores. We show that the prediction can be quite accurate, matching the actual speedups very well up to 100 parallel cores and then with a deviation of about 20% up to 256 cores.
* 10 pages, 14 figures, 5 tables. Latex ACM Sigplan format
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge