Prediction of Parallel Speed-ups for Las Vegas Algorithms

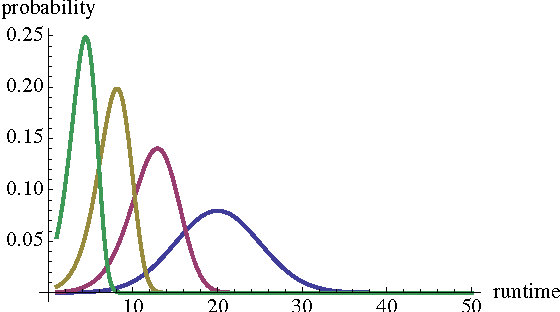
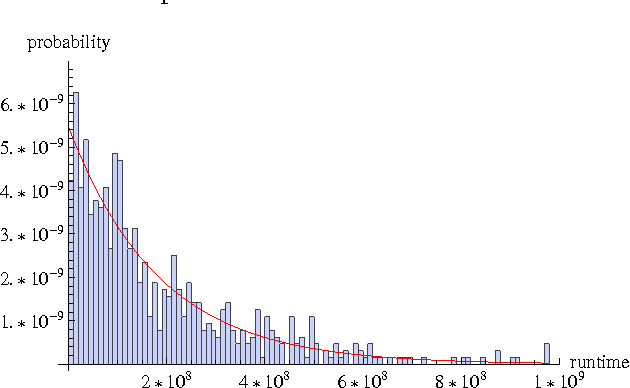
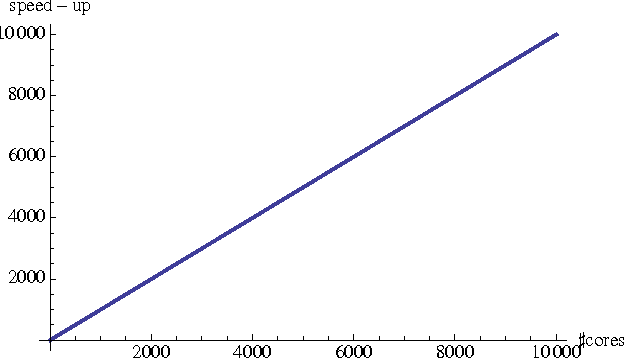
We propose a probabilistic model for the parallel execution of Las Vegas algorithms, i.e., randomized algorithms whose runtime might vary from one execution to another, even with the same input. This model aims at predicting the parallel performances (i.e., speedups) by analysis the runtime distribution of the sequential runs of the algorithm. Then, we study in practice the case of a particular Las Vegas algorithm for combinatorial optimization, on three classical problems, and compare with an actual parallel implementation up to 256 cores. We show that the prediction can be quite accurate, matching the actual speedups very well up to 100 parallel cores and then with a deviation of about 20% up to 256 cores.

On the Implementation of GNU Prolog

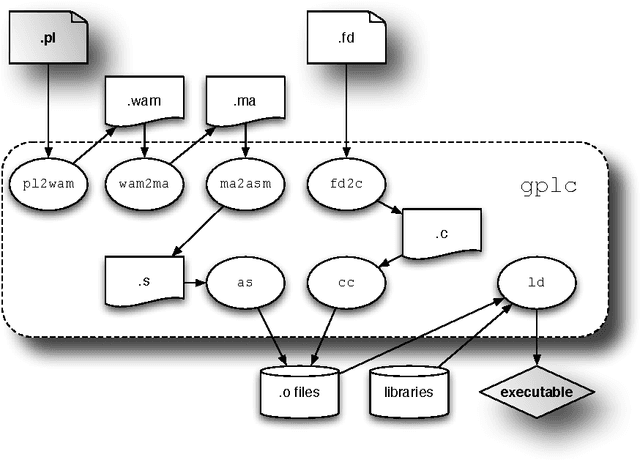
GNU Prolog is a general-purpose implementation of the Prolog language, which distinguishes itself from most other systems by being, above all else, a native-code compiler which produces standalone executables which don't rely on any byte-code emulator or meta-interpreter. Other aspects which stand out include the explicit organization of the Prolog system as a multipass compiler, where intermediate representations are materialized, in Unix compiler tradition. GNU Prolog also includes an extensible and high-performance finite domain constraint solver, integrated with the Prolog language but implemented using independent lower-level mechanisms. This article discusses the main issues involved in designing and implementing GNU Prolog: requirements, system organization, performance and portability issues as well as its position with respect to other Prolog system implementations and the ISO standardization initiative.

Parallel local search for solving Constraint Problems on the Cell Broadband Engine (Preliminary Results)

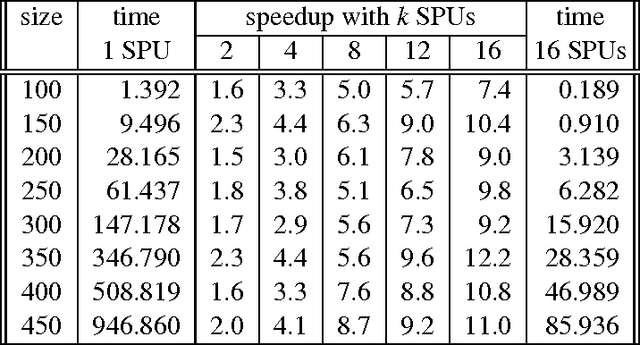
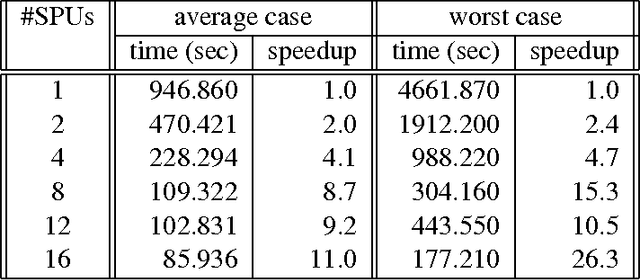
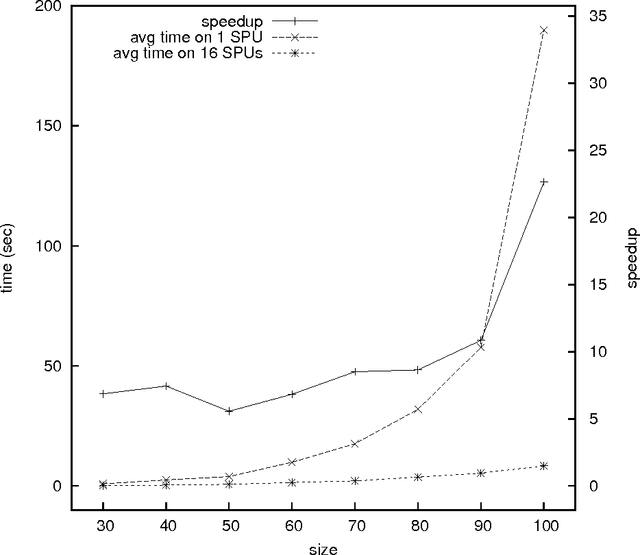
We explore the use of the Cell Broadband Engine (Cell/BE for short) for combinatorial optimization applications: we present a parallel version of a constraint-based local search algorithm that has been implemented on a multiprocessor BladeCenter machine with twin Cell/BE processors (total of 16 SPUs per blade). This algorithm was chosen because it fits very well the Cell/BE architecture and requires neither shared memory nor communication between processors, while retaining a compact memory footprint. We study the performance on several large optimization benchmarks and show that this achieves mostly linear time speedups, even sometimes super-linear. This is possible because the parallel implementation might explore simultaneously different parts of the search space and therefore converge faster towards the best sub-space and thus towards a solution. Besides getting speedups, the resulting times exhibit a much smaller variance, which benefits applications where a timely reply is critical.