Constraint Model for the Satellite Image Mosaic Selection Problem

Satellite imagery solutions are widely used to study and monitor different regions of the Earth. However, a single satellite image can cover only a limited area. In cases where a larger area of interest is studied, several images must be stitched together to create a single larger image, called a mosaic, that can cover the area. Today, with the increasing number of satellite images available for commercial use, selecting the images to build the mosaic is challenging, especially when the user wants to optimize one or more parameters, such as the total cost and the cloud coverage percentage in the mosaic. More precisely, for this problem the input is an area of interest, several satellite images intersecting the area, a list of requirements relative to the image and the mosaic, such as cloud coverage percentage, image resolution, and a list of objectives to optimize. We contribute to the constraint and mixed integer lineal programming formulation of this new problem, which we call the \textit{satellite image mosaic selection problem}, which is a multi-objective extension of the polygon cover problem. We propose a dataset of realistic and challenging instances, where the images were captured by the satellite constellations SPOT, Pl\'eiades and Pl\'eiades Neo. We evaluate and compare the two proposed models and show their efficiency for large instances, up to 200 images.

Modular Constraint Solver Cooperation via Abstract Interpretation

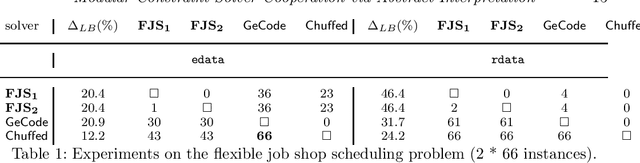
Cooperation among constraint solvers is difficult because different solving paradigms have different theoretical foundations. Recent works have shown that abstract interpretation can provide a unifying theory for various constraint solvers. In particular, it relies on abstract domains which capture constraint languages as ordered structures. The key insight of this paper is viewing cooperation schemes as abstract domains combinations. We propose a modular framework in which solvers and cooperation schemes can be seamlessly added and combined. This differs from existing approaches such as SMT where the cooperation scheme is usually fixed (e.g., Nelson-Oppen). We contribute to two new cooperation schemes: (i) interval propagators completion that allows abstract domains to exchange bound constraints, and (ii) delayed product which exchanges over-approximations of constraints between two abstract domains. Moreover, the delayed product is based on delayed goal of logic programming, and it shows that abstract domains can also capture control aspects of constraint solving. Finally, to achieve modularity, we propose the shared product to combine abstract domains and cooperation schemes. Our approach has been fully implemented, and we provide various examples on the flexible job shop scheduling problem. Under consideration for acceptance in TPLP.