Procedural Fairness in Machine Learning

Fairness in machine learning (ML) has received much attention. However, existing studies have mainly focused on the distributive fairness of ML models. The other dimension of fairness, i.e., procedural fairness, has been neglected. In this paper, we first define the procedural fairness of ML models, and then give formal definitions of individual and group procedural fairness. We propose a novel metric to evaluate the group procedural fairness of ML models, called $GPF_{FAE}$, which utilizes a widely used explainable artificial intelligence technique, namely feature attribution explanation (FAE), to capture the decision process of the ML models. We validate the effectiveness of $GPF_{FAE}$ on a synthetic dataset and eight real-world datasets. Our experiments reveal the relationship between procedural and distributive fairness of the ML model. Based on our analysis, we propose a method for identifying the features that lead to the procedural unfairness of the model and propose two methods to improve procedural fairness after identifying unfair features. Our experimental results demonstrate that we can accurately identify the features that lead to procedural unfairness in the ML model, and both of our proposed methods can significantly improve procedural fairness with a slight impact on model performance, while also improving distributive fairness.

EFFL: Egalitarian Fairness in Federated Learning for Mitigating Matthew Effect

Recent advances in federated learning (FL) enable collaborative training of machine learning (ML) models from large-scale and widely dispersed clients while protecting their privacy. However, when different clients' datasets are heterogeneous, traditional FL mechanisms produce a global model that does not adequately represent the poorer clients with limited data resources, resulting in lower accuracy and higher bias on their local data. According to the Matthew effect, which describes how the advantaged gain more advantage and the disadvantaged lose more over time, deploying such a global model in client applications may worsen the resource disparity among the clients and harm the principles of social welfare and fairness. To mitigate the Matthew effect, we propose Egalitarian Fairness Federated Learning (EFFL), where egalitarian fairness refers to the global model learned from FL has: (1) equal accuracy among clients; (2) equal decision bias among clients. Besides achieving egalitarian fairness among the clients, EFFL also aims for performance optimality, minimizing the empirical risk loss and the bias for each client; both are essential for any ML model training, whether centralized or decentralized. We formulate EFFL as a constrained multi-constrained multi-objectives optimization (MCMOO) problem, with the decision bias and egalitarian fairness as constraints and the minimization of the empirical risk losses on all clients as multiple objectives to be optimized. We propose a gradient-based three-stage algorithm to obtain the Pareto optimal solutions within the constraint space. Extensive experiments demonstrate that EFFL outperforms other state-of-the-art FL algorithms in achieving a high-performance global model with enhanced egalitarian fairness among all clients.

Voronoi-based Efficient Surrogate-assisted Evolutionary Algorithm for Very Expensive Problems

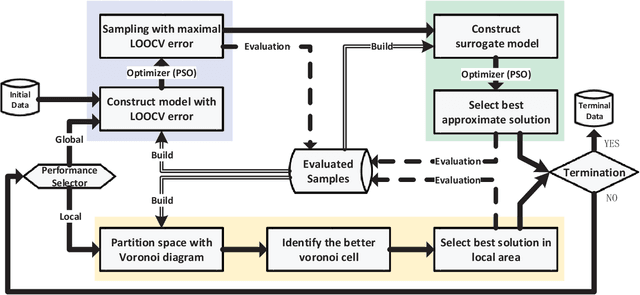
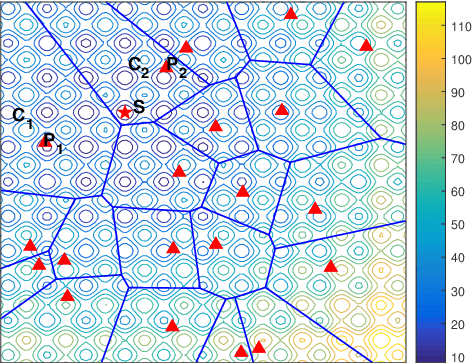
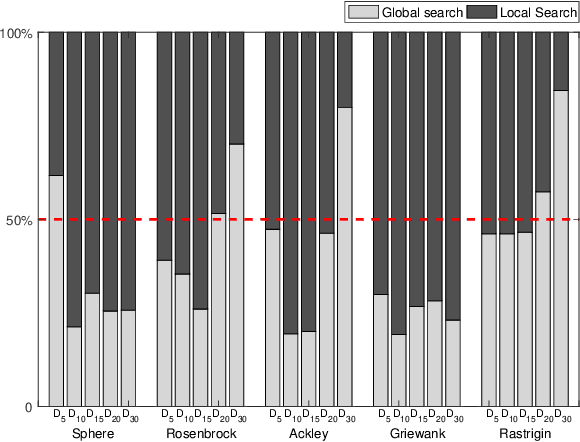
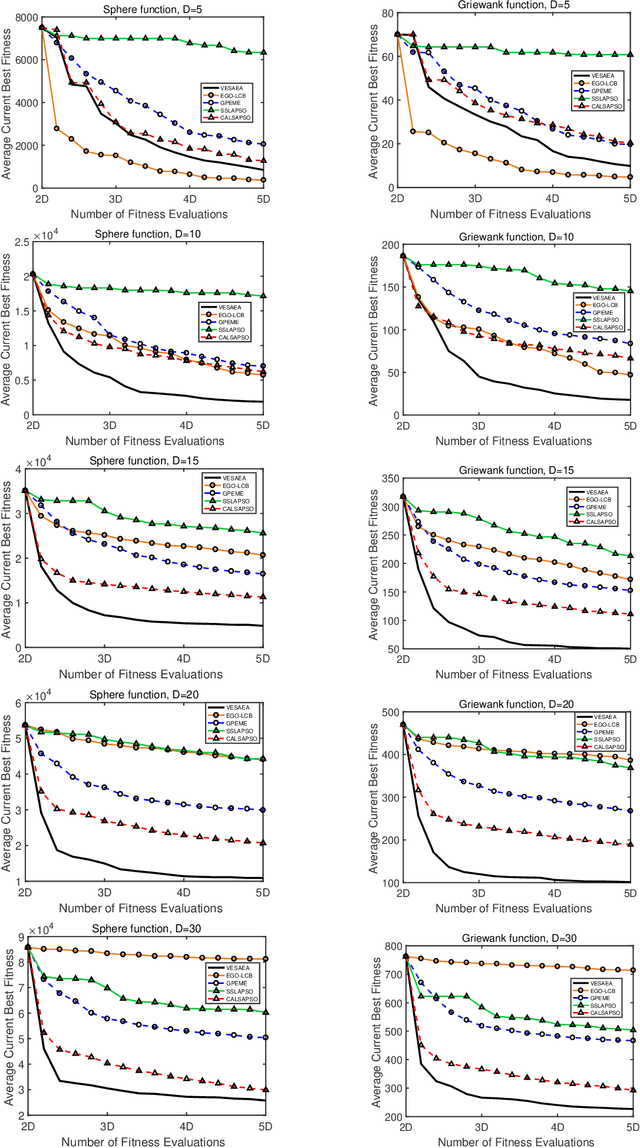
Very expensive problems are very common in practical system that one fitness evaluation costs several hours or even days. Surrogate assisted evolutionary algorithms (SAEAs) have been widely used to solve this crucial problem in the past decades. However, most studied SAEAs focus on solving problems with a budget of at least ten times of the dimension of problems which is unacceptable in many very expensive real-world problems. In this paper, we employ Voronoi diagram to boost the performance of SAEAs and propose a novel framework named Voronoi-based efficient surrogate assisted evolutionary algorithm (VESAEA) for very expensive problems, in which the optimization budget, in terms of fitness evaluations, is only 5 times of the problem's dimension. In the proposed framework, the Voronoi diagram divides the whole search space into several subspace and then the local search is operated in some potentially better subspace. Additionally, in order to trade off the exploration and exploitation, the framework involves a global search stage developed by combining leave-one-out cross-validation and radial basis function surrogate model. A performance selector is designed to switch the search dynamically and automatically between the global and local search stages. The empirical results on a variety of benchmark problems demonstrate that the proposed framework significantly outperforms several state-of-art algorithms with extremely limited fitness evaluations. Besides, the efficacy of Voronoi-diagram is furtherly analyzed, and the results show its potential to optimize very expensive problems.